Lernziele
- Sie können einfache Programme nachvollziehen und auf Fehler untersuchen
- Sie finden für einfache Aufgabenstellungen algorithmische Lösungen und können diese in einer Programmiersprache implementieren
- Sie können einfache Modelle entwickeln und in einer Computersimulation implementieren
Sinn und Zweck
Ein Ziel der Wissenschaft ist es, komplexe System wie beispielsweise das Wetter, das menschliche Gehirn oder die Volkswirtschaft eines Staates kennenzulernen und ihre Reaktionen auf gewisse Einflüsse vorhersagen zu können. Nicht immer ist es aber möglich, diese Experimente direkt am realen Objekt durchzuführen. Hat das zu untersuchende System beispielsweise die Grösse von Planeten oder ist es so klein wie Moleküle, dauern Veränderungen so lang wie gewisse Evolutionsprozesse oder so kurz wie Neuronenverschaltungen im Gehirn, bietet sich die Möglichkeit, die reale Welt in einem Computer-Modell abzubilden. Die Veränderungen eines solchen Modells, die durch die modellierte Zeit und den modellierten Raum beeinflusst werden, fallen unter den Begriff Simulation.
Geschichte
In den Naturwissenschaften gibt es verschiedene Methoden, die allein oder in verschiedenen Kombinationen zur Gewinnung neuer Erkenntnisse eingesetzt werden. Eine der wichtigsten ist die Methode der theoretischen Herleitung. Diese wurde schon ca. 600 Jahre vor Christus im antiken Griechenland entwickelt (unter anderem von Thales und Pythagoras). Über mehr als 2’000 Jahre war die Theorie die vorherrschende wissenschaftliche Methodik in den Naturwissenschaften.
Erst im 16. Jahrhundert nach Christus wurde in Europa mit Experimenten eine weitere naturwissenschaftliche Methodik entwickelt. Insbesondere Galileo Galilei trug zur Entwicklung dieser Methodik bei, zum Beispiel mit seinen Experimenten zum freien Fall im Jahre 1623. Wie in der Theorie geht auch ein Experiment von einer Fragestellung aus. Mit dieser Frage wird ein Experiment geplant, wobei versucht wird, die äusseren Einflüsse zu eliminieren und nur die Faktoren, die von Interesse sind, kontrolliert zu verändern. Dadurch kann gezeigt werden, welche Faktoren einen Einfluss haben und wie diese sich auswirken.
Im letzten Jahrhundert wurden die Naturwissenschaften um eine weitere methodologische Kategorie bereichert, welche zwischen Theorie und Experiment eingeordnet werden kann. Diese Methode besteht aus der mathematischen Modellierung und Computer-Simulation. Das Advanced Scientific Computing Committee of the US National Science Foundation schreibt 1984:
Science is undergoing a structural transition from two broad methodologies to three – namely from experimental and theoretical science to include the additional category of computational and information science. A comparable example of such change occurred with the development of systematic experimental science at the time of Galileo.
Eine der ersten Simulationen wurde 1946 im Zuge des Manhattan-Projektes auf dem ersten elektronischen Universalrechner der Welt durchgeführt. Dabei war es möglich, mit Hilfe eines Computers verschiedene Designs einer Atombombe zu testen, indem die hydrodynamischen Gleichungen mit dem Computer gelöst wurden. Dies war notwendig, da Experimente dazu nur sehr schwierig durchzuführen waren, weil während eines Fusionsprozesses sehr hohe Temperaturen und Drücke notwendig sind.
Die Simulationen wurden erst durch die ersten universellen Rechner ermöglicht, wobei diese spezifisch für die Simulation entwickelt wurden. Diese enge Verknüpfung zwischen der Entwicklung der Computertechnik und Computer-Simulationen führte dazu, dass in den letzten Jahrzehnten immer schnellere Rechner entwickelt wurden, was wiederum grössere Simulationen ermöglichte.
Diese Entwicklung führte zu vielen Durchbrüchen in der Forschung. So wurden die Begründer der Simulationsmethode Molecular Dynamics 2013 mit dem Nobelpreis für Chemie ausgezeichnet. Inzwischen ist es dank Computer-Simulationen möglich, das dynamische Verhalten von Proteinen mit weit über 100’000 Atomen zu simulieren, was zu vielen neuen Erkenntnissen führte.
Modell
Unter dem Begriff Modell versteht man eine Interpretation oder Abstraktion der realen Welt. Für Computer-Simulationen ist es notwendig, mathematische Modelle zu erstellen, bei denen eine Abstraktion der realen Welt in eine mathematische Notation notwendig ist. Da die Welt jedoch sehr komplex ist, werden beim Prozess der Modellbildung Annahmen und Vereinfachungen gemacht. Dies führt dazu, dass alle Modelle beschränkt sind, d.h. sie können die reale Welt nicht exakt abbilden. Daher wird oft davon gesprochen, ein Modell eines Systems zu erstellen. Unter dem Begriff System versteht man eine abgeschlossene Sammlung von Elementen, die miteinander verbunden sind. Beispiele für Systeme können die Welt, ein Fisch oder ein Protein sein. Da nur ein Ausschnitt der realen Welt modelliert wird, wird die Modellbildung vereinfacht.
Simulation
Um Computer-Simulationen durchzuführen, ist die Zusammenarbeit von verschiedenen Fachgebieten und Disziplinen erforderlich. Das Modell muss mathematisch beschrieben werden, da es ansonsten nicht mit Hilfe der Informatik als Simulation umgesetzt werden kann. Zusätzlich zu Kenntnissen aus Mathematik und Informatik ist ein tiefes Verständnis der Disziplin, in der man simulieren möchte, unerlässlich. Denn ohne Wissen aus dieser Disziplin ist es schwierig, das Modell korrekt zu erstellen oder die Ergebnisse der Simulation zu interpretieren.
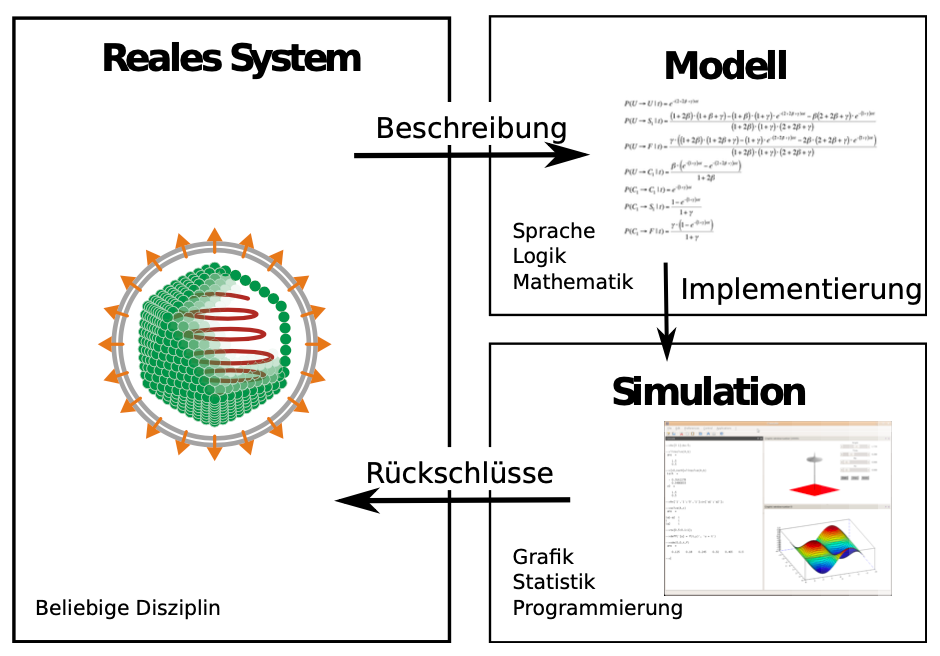
Simulationen dienen dazu, das Verhalten von Systemen zu analysieren. Hierfür muss man zuerst ein mathematisches Modell dieses Systems erstellen. Dieses mathematische Modell kann dann als Simulation implementiert werden. Bei der Implementierung eines Modells wird dieses von der mathematischen Sprache in eine Notation umgewandelt, die ein Computer interpretieren kann. Dies kann eine Darstellung des Modells in einer Programmiersprache sein. Nachdem das mathematische Modell im Computer implementiert wurde, kann es simuliert werden. Dabei wird das mathematische Modell mit verschiedenen Eingabeparametern gestartet, um das Verhalten des Systems über eine Zeit zu analysieren. Eine Simulation wird also durch die Eingabeparameter und das implementierte mathematische Modell definiert. Die Simulation selbst wird vom Computer automatisch durchgeführt, wobei die Ergebnisse protokolliert werden, sodass sie nachträglich analysiert werden können. Um das Verhalten des Systems visuell zu analysieren, kommen geeignete visuelle Darstellungen der Resultate zum Einsatz. Das Ziel von Simulationen kann sein, dass man mehr über das Verhalten des modellierten Systems verstehen oder verschiedene Strategien für die Funktionsweise des Systems vergleichen will.
Validierung
Nach der Durchführung einer Simulation ist es notwendig, die Daten der Simulation zu validieren. Eine Möglichkeit die Daten zu validieren, ist der Vergleich mit Daten, welche in Experimenten gewonnen wurden.
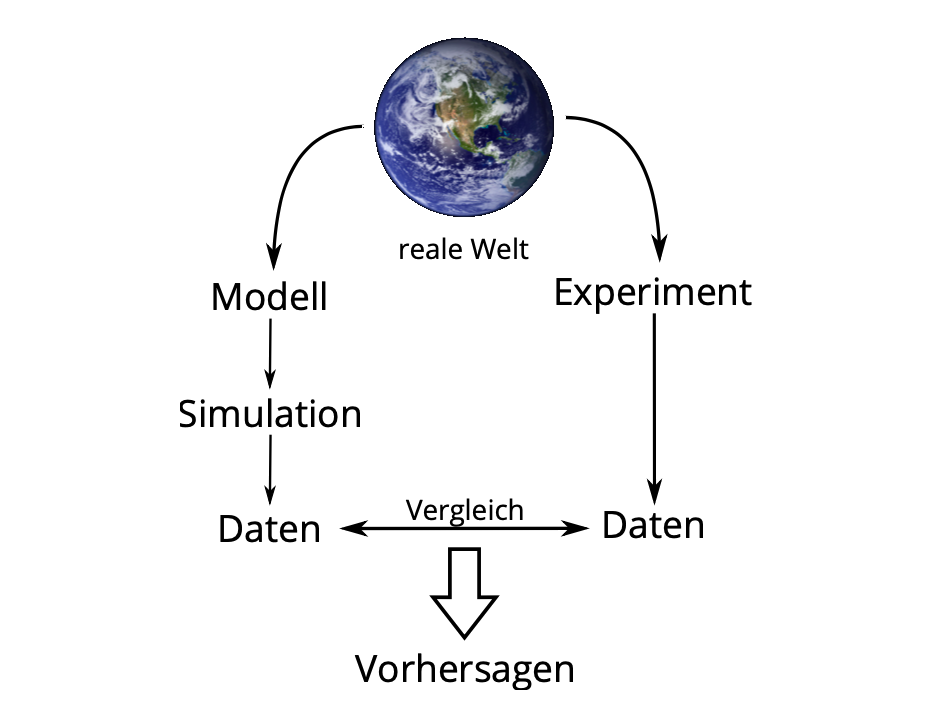
Die Datenvalidierung ist erforderlich, damit die Ergebnisse nicht falsch oder überinterpretiert werden und man die Grenzen der Simulation und des Modells erkennt. Die Methodik des Modellieren und Simulieren hat verschiedene Fehlerquellen, die nicht vernachlässigt werden dürfen. Die grösste Fehlerquelle liegt meist im Prozess der Modellbildung. Man darf nicht vergessen, dass ein Modell nur eine reduzierte Abbildung der Wirklichkeit ist. Daher kann ein Modell nur Aussagen über die Aspekte liefern, die bei der Modellbildung berücksichtigt wurden. Eine weitere Fehlerquelle ist die Implementierung des mathematischen Modells, da Computer Einschränkungen mit sich bringen. So ist zum Beispiel der Zahlenraum von Computern endlich, was zu verschiedenen numerischen Problemen führen kann.
Die Kapitel «Sinn und Zweck», «Geschichte», «Modell», «Simulation» und «Validierung» basierend auf «Modellieren und Simulieren» von Lukas Fässler und David Sichau