Wenn wir Schaltungen konstruieren gilt es folgendes zu beachten:
- Keine direkten Verbindungen vom Plus- zum Minuspol. Sonst Kurzschluss!
- Der Ausgang ist immer entweder mit dem Minus- oder aber dem Pluspol verbunden. Sonst befindet sich die Schaltung in einem undefinierten Zustand.
Im Folgenden werden wir drei Schaltungen kennen lernen. Zu jeder der drei Schaltungen existiert eine mathematische Operation, welche durch die Schaltung auf die Eingangswerte angewendet wird und einen Wert für den Ausgang zur Folge hat. Daneben können wir diesen Schaltungen auch logische Funktionen, wie wir sie z.B. beim Zusammensetzen von Wahrheitswerten beim Programmieren verwenden, zuweisen.
Mögliche Ein- und Ausgangswerte:
- Mit Pluspol verbunden = 1
- Mit Minuspol verbunden = 0
# Negation / NICHT (NOT)
Die einfachste Schaltung die etwas berechnet ist hier abgebildet:
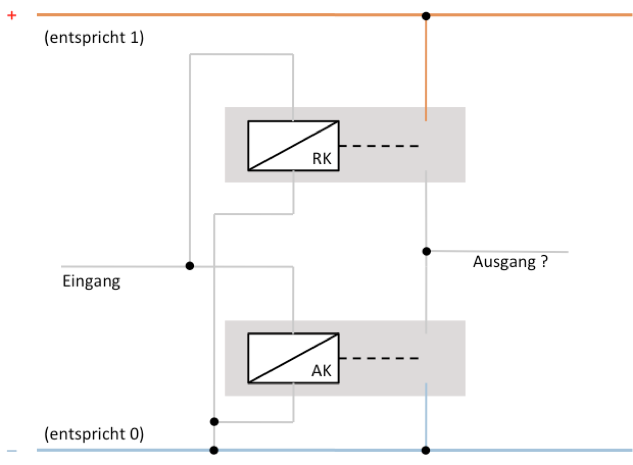
Verbindet man den Eingang mit dem Minuspol, so bleiben beide Relais im passiven Zustand. Der Ausgang ist mit dem Pluspol verbunden.
Verbindet man den Eingang mit dem Pluspol, so fliesst durch beide Relais Strom. Sie sind nun im aktiven Zustand. Dabei öffnet das Relais mit Ruhekontakt den Schalter und trennt somit den Ausgang vom Pluspol, wogegen das Relais mit Arbeitskontakt den Schalter schliesst und den Ausgang mit dem Minuspol verbindet.
Unsere Überlegungen zu möglichen Eingangswerten und den dazugehörigen Werten beim Ausgang können wir in einer Tabelle festhalten:
| Eingang | Ausgang |
|---|---|
| 0 | 1 |
| 1 | 0 |
Die Tabelle beschreibt eine mathematische/logische Operation. Es handelt sich um die Negation: aus 0 wird 1 und aus 1 wird 0.
| A | NOT A |
|---|---|
| 0 | 1 |
| 1 | 0 |
# Multiplikation / UND (AND)
Die folgende Schaltung ist schon etwas komplizierter. Sie besteht aus vier Relais die durch zwei Eingänge geschaltet werden und einen Ausgang steuern.
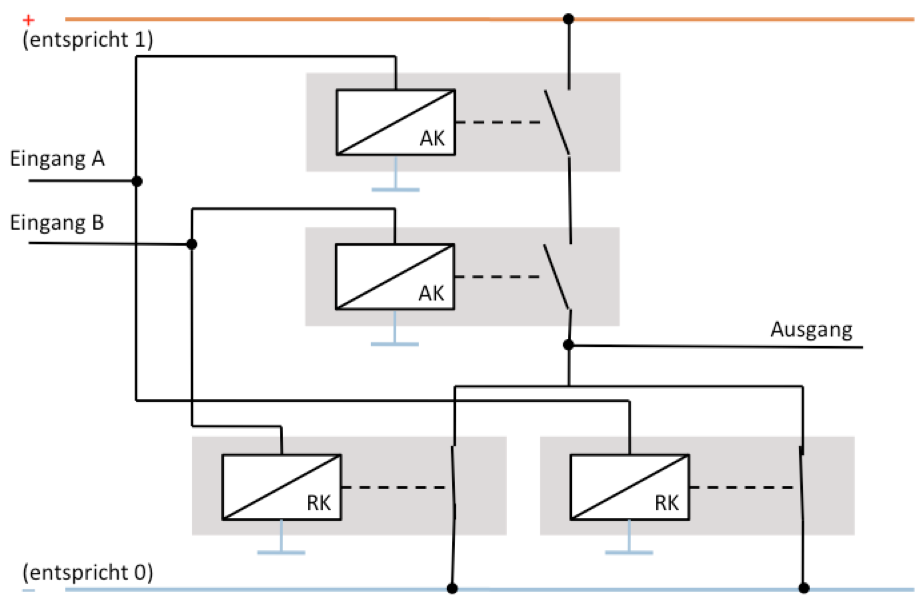
Tabelle aller möglichen Eingänge mit Ergebnis:
| Eingang A | Eingang B | Ausgang |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Dies entspricht einer weiteren uns bekannten Operation, nämlich der Multiplikation, respektive der UND-Operation.
| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
# Addition / exklusives ODER (XOR)
Die folgende Schaltung ist sogar noch komplizierter. Mit ihr lässt sich das sogenannte «exklusive ODER» (XOR) implementieren: Der Ausgang ist genau dann 1 wenn genau einer der beiden Eingangswerte 1 ist. Sonst ist der Ausgangswert 0.
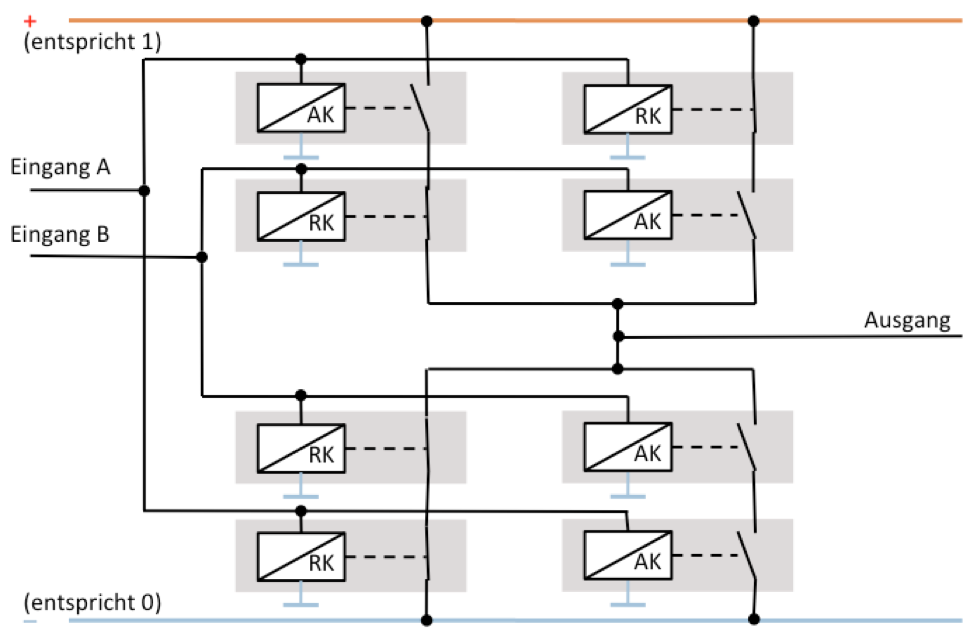
Tabelle aller möglichen Eingänge mit Ergebnis:
| Eingang A | Eingang B | Ausgang |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Bis auf die letzte Zeile entspricht das der Addition. Für eine Addition fehlt der Übertrag. (Dazu müsste die Schaltung aber zwei Ausgänge haben.)
| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
# Module
Vorhandene logische Schaltungen werden in Modulen verbaut. So könnten wir ein UND- und auch ein XOR-Modul konstruieren, welche wir dann wiederum in komplizierteren Schaltungen einsetzen. Beide Module besitzen fünf Anschlüsse: einer für den Plus- und einer für den Minuspol der Stromquelle, sowie zwei Eingänge und ein Ausgang.
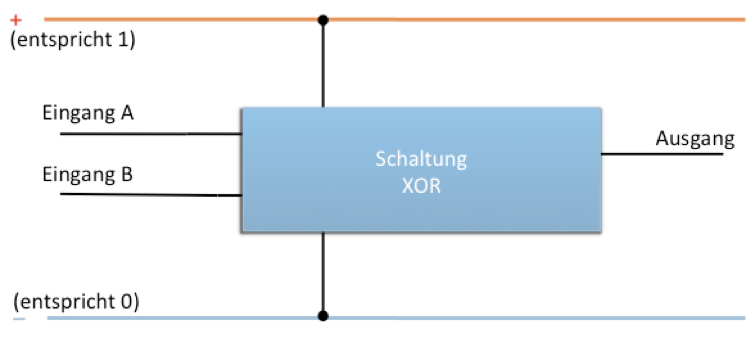
Damit der «Bauplan» einer komplexeren Schaltung nicht allzu viele Verbindungslinien aufweist, lässt man die Anschlüsse zu Plus- und Minuspol jeweils weg. Wenn man die Schaltung aber mit echten Teilen zusammenbaut, sind diese Verbindungen zwingend nötig!

Aufgabe
Baue in Zweiergruppen mit dem Logikbaukasten die AND- und die XOR-Schaltung nach
- Verwende als Eingang zwei Schiebeschalter
- Am Ausgang kannst du eine Leuchtdiode (LED) anschliessen
Achtung: die Diode muss über einen Widerstand mit dem Minuspol verbunden werden!