Einführung: Die Collatz-Vermutung

Das Collatz-Problem wurde vom deutschen Mathematiker Lothar Collatz im Jahre 1937 aufgestellt. Es ist im Grunde ein mathematisches Problem, eignet sich aber wunderbar zur Illustration von Berechenbarkeitsproblemen in der Informatik. Das Problem wird mathematisch wie folgt definiert:

Das Collatz-Problem ist ein bis heute ungelöstes Problem. Es wurde schon als «absolut hoffnungslos» und als «Sumpf» bezeichnet, als Problem aus «der dunklen Ecke» der Mathematik, als Problem, für das die Mathematik noch nicht bereit ist. Das Problem wird deshalb offiziell auch Collatz-Vermutung genannt (Englisch: Collatz conjecture). Aber was genau ist eigentlich das Collatz-Problem?

Aufgabe: Die Collatz-Vermutung

Probieren Sie die Collatz-Funktion aus:

• Wählen Sie eine beliebige natürliche Zahl 𝑛 > 0. Notieren Sie die Zahl.
• Wenn 𝑛 gerade ist, dann ist die folgende Zahl 𝑛/2. Notieren Sie die Zahl.
• Wenn 𝑛 ungerade ist, dann ist die folgende Zahl 3𝑛 + 1. Notieren Sie die Zahl.
• Wiederholen Sie diese Vorgehensweise mit den folgenden Zahlen. Schreiben Sie die erhaltenen Zahlen als Folge auf.

Diskutieren Sie kurz und notieren Sie eine Gruppenantwort zu folgenden Fragen:

1. Wenn Sie der Anweisung folgen, was stellen Sie fest? Was ist das «Ergebnis»?
2. Finden Sie das Problem schwer? Was könnte das heissen, dass das Problem bis heute nicht gelöst wurde? Was ist überhaupt «das Problem», was versucht man zu lösen?
3. Überlegen Sie: was könnte die Collatz-Vermutung sein? Was wird da wohl «vermutet»?

Darstellung beispielhafter Zahlenfolgen, die durch Anwendung des Collatz-Algorithmus entstehen.

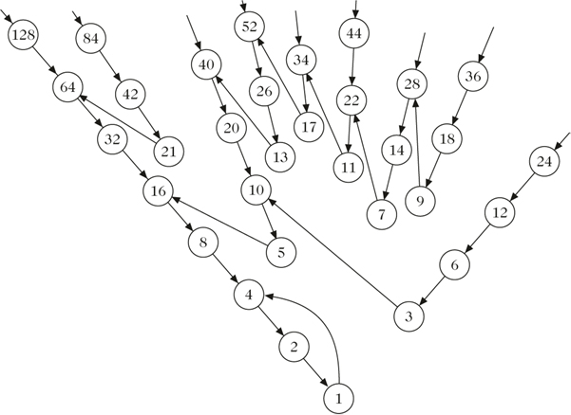
Die Collatz-Vermutung besagt, dass mit Anwendung des oben beschriebenen Algorithmus, für alle natürlichen Zahlen, schlussendlich immer die Zahl 1 resultiert (bzw. die sich wiederholende Zahlenfolge 4-2-1). Man vermutet also, dass dies tatsächlich für jede beliebige positive natürliche Zahl gilt. Aber gibt es Ausnahmen? Bis heute hat niemand eine Zahl gefunden, die der Collatz-Vermutung widerspricht. Die erste Person, die eine Zahl finden würde, mit der man durch Anwendung des Collatz-Algorithmus nicht bei 1 enden würde, hätte das Collatz-Problem gelöst und den Beweis geliefert, dass die Vermutung falsch ist.

Diverse Forschende haben mit «Brute-Force-Methoden» Trillionen (10¹⁸) von Startwerten getestet und festgestellt, dass alle dabei entstandenen Collatz-Folgen mit 1 enden. Der Mathematiker Terence Tao im Jahr 2019 das bisher bedeutendste Ergebnis liefern können. Mit vielen komplexen Annahmen und Verfeinerungen konnte Terence Tao zeigen, dass 99% aller Startwerte, die grösser einer Billiarde (10¹⁵) sind, durch Anwendung des Collatz-Algorithmus irgendwann eine Zahl unter 200 erreichen, und damit auch irgendwann eine 1. Er konnte aber keine Zahl finden, die der Collatz-Vermutung widerspricht, und damit die Vermutung auch nicht widerlegen. «Man kann der Vermutung so nahekommen, wie man will, doch sie bleibt immer ausser Reichweite», sagte Terence Tao nach der Veröffentlichung seines Ansatzes und warnte: «[Man kann dabei] viel Zeit verschwenden».

Collatz-Vermutung: Umsetzung mit Python

Seit bald 100 Jahren fasziniert die Collatz-Vermutung Menschen auf der ganzen Welt und lässt sie alle verzweifeln. Zum Erkunden von Eigenschaften bietet sich eine Umsetzung mit Python an, da dies die Analyse auch von sehr grossen Startwerten und von aussergewöhnlichen Collatz-Folgen erlaubt.

Aufgabe: Collatz-Funktion implementieren

Implementieren Sie den untenstehenden Python-Code der Collatz-Funktion.

Lösung: Collatz-Funktion

Python-Code: Darstellung von Collatz-Folgen

def collatz(n):
	while n > 1:
		print(n, end=' ')   # end=' ' heisst: beim print keine neue Zeile beginnen
		if (n % 2 == 0):    # n ist gerade
			n = n//2
		else:               # n ist ungerade 
			n = 3*n + 1
	print(1)

n = int(input('Geben Sie eine natürliche Zahl n an: '))
print('Collatz-Folge: ')
collatz(n)

Aufgabe: Eigenschaften der Collatz-Folge

Testen Sie Ihren Algorithmus: Was passiert bei Eingabe einer ungültigen Zahl?

Aufgabe: Eigenschaften der Collatz-Folge

1. Überprüfen Sie, mit Hilfe des Python-Codes folgende Eigenschaften.
   Eine der aufgeführten Eigenschaften ist falsch, welche?

   1. Keine Zahl taucht in einer Collatz-Folge zweimal auf.
   2. Auf eine ungerade Zahl folgt immer eine gerade Zahl.
   3. Die Zahlen 5 und 32 führen zur gleichen Collatz-Folge.
   4. Auf eine gerade Zahl folgt immer eine ungerade Zahl.

2. Es gibt bestimmte Startwerte, bei denen sich ganz aussergewöhnliche Collatz-Folgen entwickeln. Probieren Sie einige aus: 27, 255, 447, 639, 703. Was fällt auf?

3. Erweitern Sie das Programm als Variante so, dass alle Collatz-Folgen bis zu einer Zahl n_max ausgerechnet werden.

Aufgabe: Laufzeit von Collatz-Folgen

Ergänzen Sie den Code von oben mit einem Zähler, so dass Sie die Laufzeit des Collatz-Algorithmus ausgeben können. (Blenden Sie die Anzeige der Schritte aus und geben Sie nur die Anzahl Schritte an.)

1. Vergleichen Sie die Laufzeit von unterschiedlichen Startwerten. Wählen Sie dabei auch sehr grosse Zahlen (z.B. 10¹⁸ und grösser).
2. Herausforderung: wer findet den Startwert mit maximal 18 Stellen (10¹⁸) und mit der längsten (endlichen) Laufzeit, bis die Collatz-Folge die Zahl 1 erreicht?
3. Fortgeschrittene Aufgabe: Generieren Sie viele zufällige grosse Zahlen und weisen Sie am Schluss diejenige Zahl aus, welche die längste Collatz-Laufzeit von allen Zahlen aufweist.

Aufgabe: Grafische Darstellung von Collatz-Folgen

Die Werte einer Collatz-Folge können von der Start-Zahl ausgehend unregelmässig schwankend steigen, bevor sie dann irgend einmal unweigerlich gegen 1 tendieren werden (unbewiesen!).

1. Stellen Sie die Werte einer Collatz-Folge grafisch dar.
2. Stellen Sie die Schrittanzahl (Laufzeit) für Collatz-Folgen bis zur Zahl n_max grafisch dar.