Die Spieltheorie ist ein Zweig der Mathematik. Es geht dabei um Strategien, deren Erfolg nicht nur vom eigenen Handeln, sondern auch von Aktionen anderer abhängt.
Spieltheorie wird in den Wirtschaft-, Rechts- und Politikwissenschaften, aber auch in der Psychologie, Soziologie und Biologie eingesetzt.
In der Informatik, können die Algorithmen der Spieltheorie implementiert werden. Z.B. um einen Computergegner im Tic-tac-toe oder im Schach zu erstellen.
Minimax
Der Minimax-Algorithmus optimiert die Spielzüge unter der Annahme, dass der Gegner auch immer optimal spielt. Dazu wird ein Spielbaum erstellt, der ab der aktuellen Spielposition alle möglichen Züge erfasst. Der Baum kommt in einer Tiefe zu einer Bewertung: Entweder der Spieler gewinnt oder der Spieler verliert. Häufig kann nicht der gesamte Spielbaum berechnet werden. In diesem Fall wird in einer endlichen Tiefe eine Bewertungsfunktion angewandt.
Nun kann der Algorithmus die Bewertung zurückrechnen: Ist der Spieler am Zug, wird der grösste Wert der möglichen Werte (max) übernommen (entspricht dem besten Zug des Spielers). Ist der Gegner am Zug, dann wird der kleinste Wert (min) übernommen (entspricht dem besten Zug des Gegners).
Beispiel
Der folgende Baum stellt die Ausgangslage dar. Zu oberst (Ebene 0) ist die aktuelle Spielposition – momentan ist der Spieler an der Reihe (max) und er kann 2 verschiedene Züge machen.
Wir möchten nun entscheiden, welchen Zug der Spieler machen soll. Dazu vervollständigen wir den Baum bis z.B. Ebene 4. Die Spieler sind immer abwechslungsweise an der Reihe und es gibt 1 oder 2 mögliche Züge.
Auf Ebene 4 haben wir eine Bewertungsfunktion: Entweder gewinnt der Spieler (+∞) oder es gewinnt der Gegner (-∞) oder die Position wird mit einer Zahl bewertet.
Der Algorithmus geht beim ersten Ast ganz nach unten und führt die Werte jeweils eine Ebene nach oben. Dabei wird der kleinste oder der grösste Wert genommen, je nachdem ob der Gegner (min) oder der Spieler (max) an der Reihe sind. Sind alle Nachkommen des Knotens berechnet, kann der Knoten selbst berechnet werden. Sonst werden die Nachkommen berechnet.
Die roten Pfeile zeigen nun «den Weg» der besten Position, nämlich die -7 auf der rechten Seite an.
Implementation
Der Algorithums lässt sich am besten rekursiv implementieren:
Minimax des ganzen Baumes ist das Maximum (oder Minimum) aller Minimax der Kinder (nächste Ebene), usw.
Natürlich müssen wir die Rekursion verankern, so dass der Algorithmus irgendwann stoppt. Dies geschieht, wenn wir auf der untersten Ebene mit den bereits berechneten Werten ankommen. Hier müssen wir nicht mehr Minimax-Aufrufen.
Aufgabe
Aufgabe: Minimax
Lösen Sie den Baum mit Hilfe von alpha-beta-pruning. (rot=minimierend, grün=maximierend)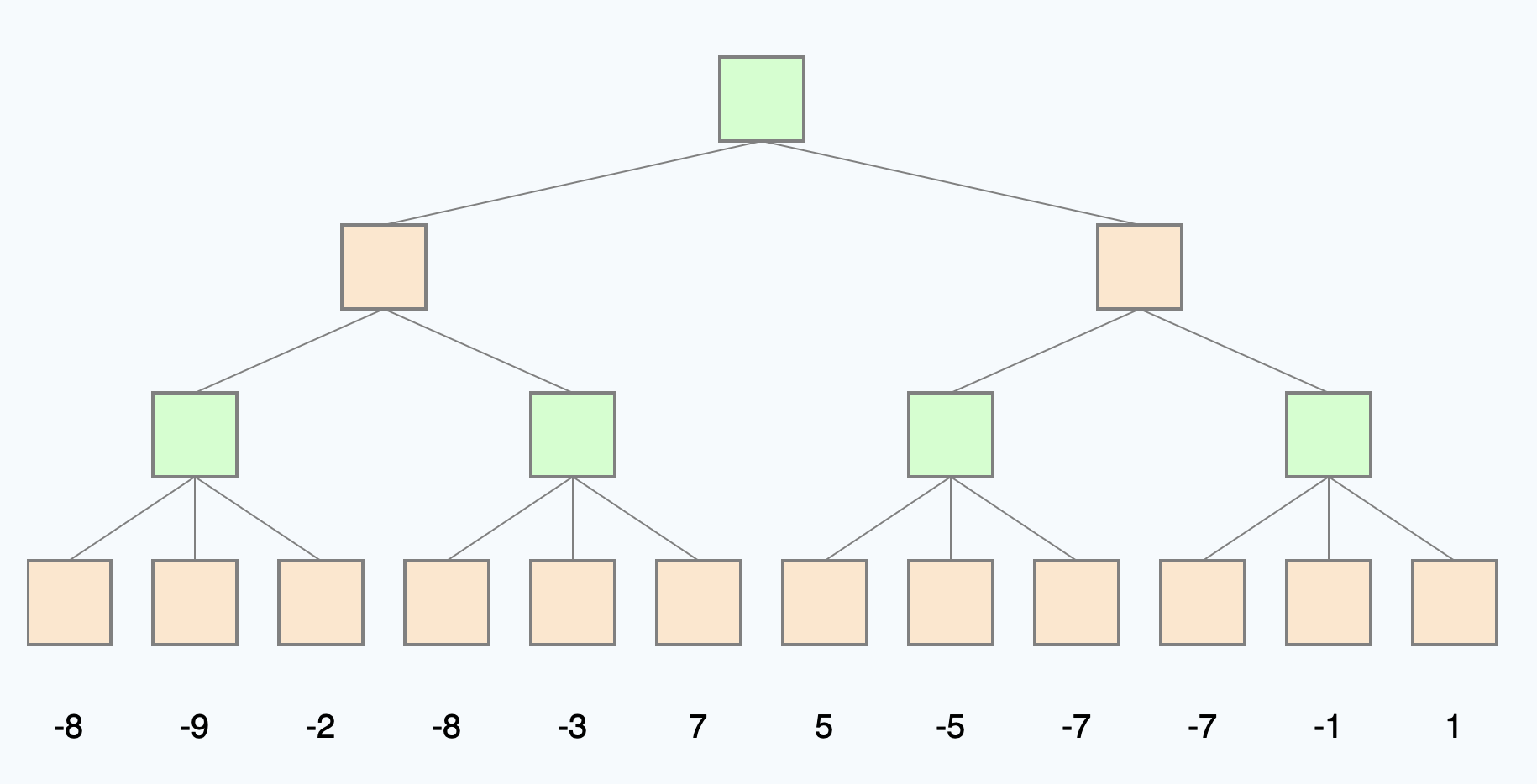
Weitere Beispiele interaktiv lösbar auf:
👉 https://www.yosenspace.com/posts/computer-science-game-trees.html
Lösung
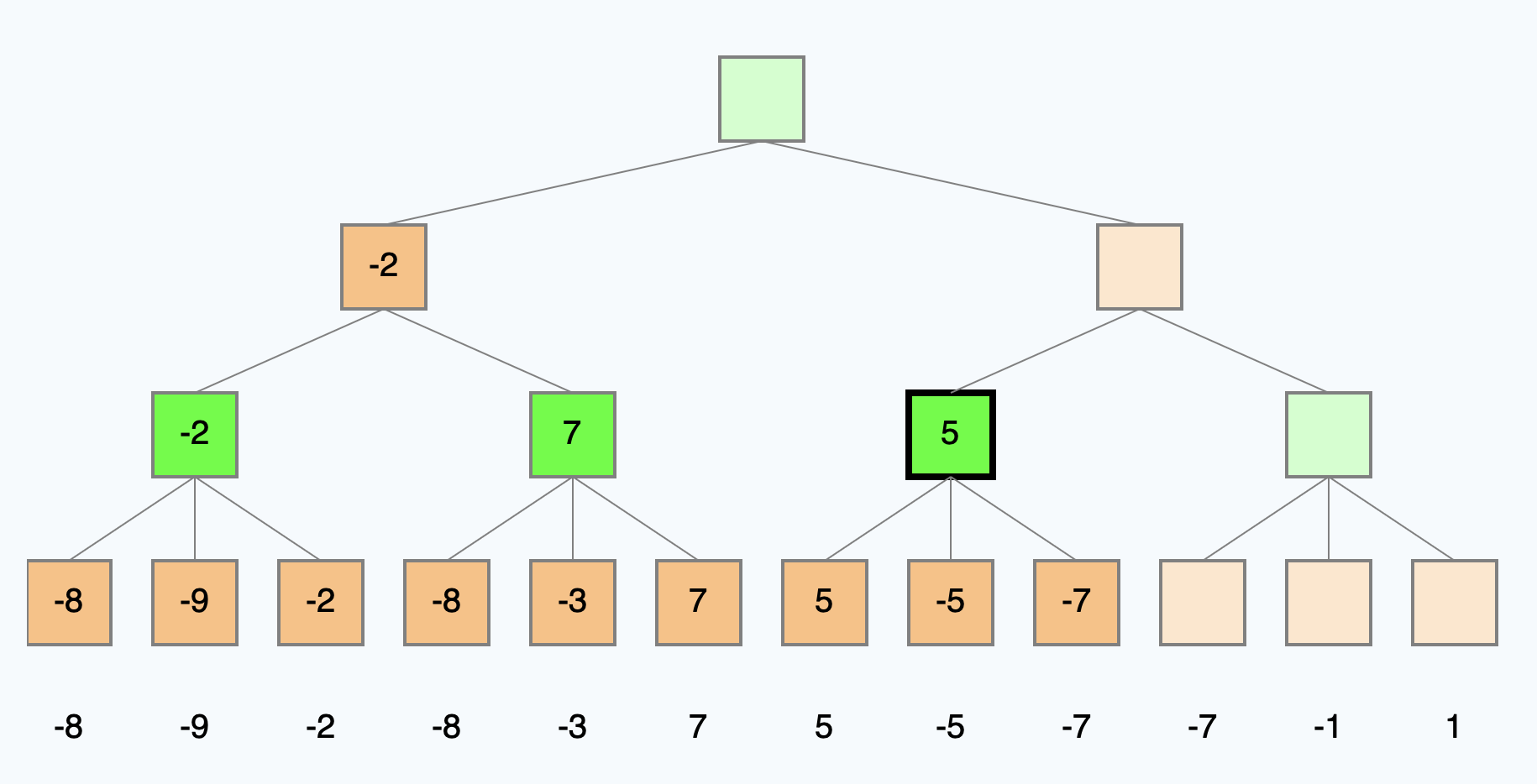
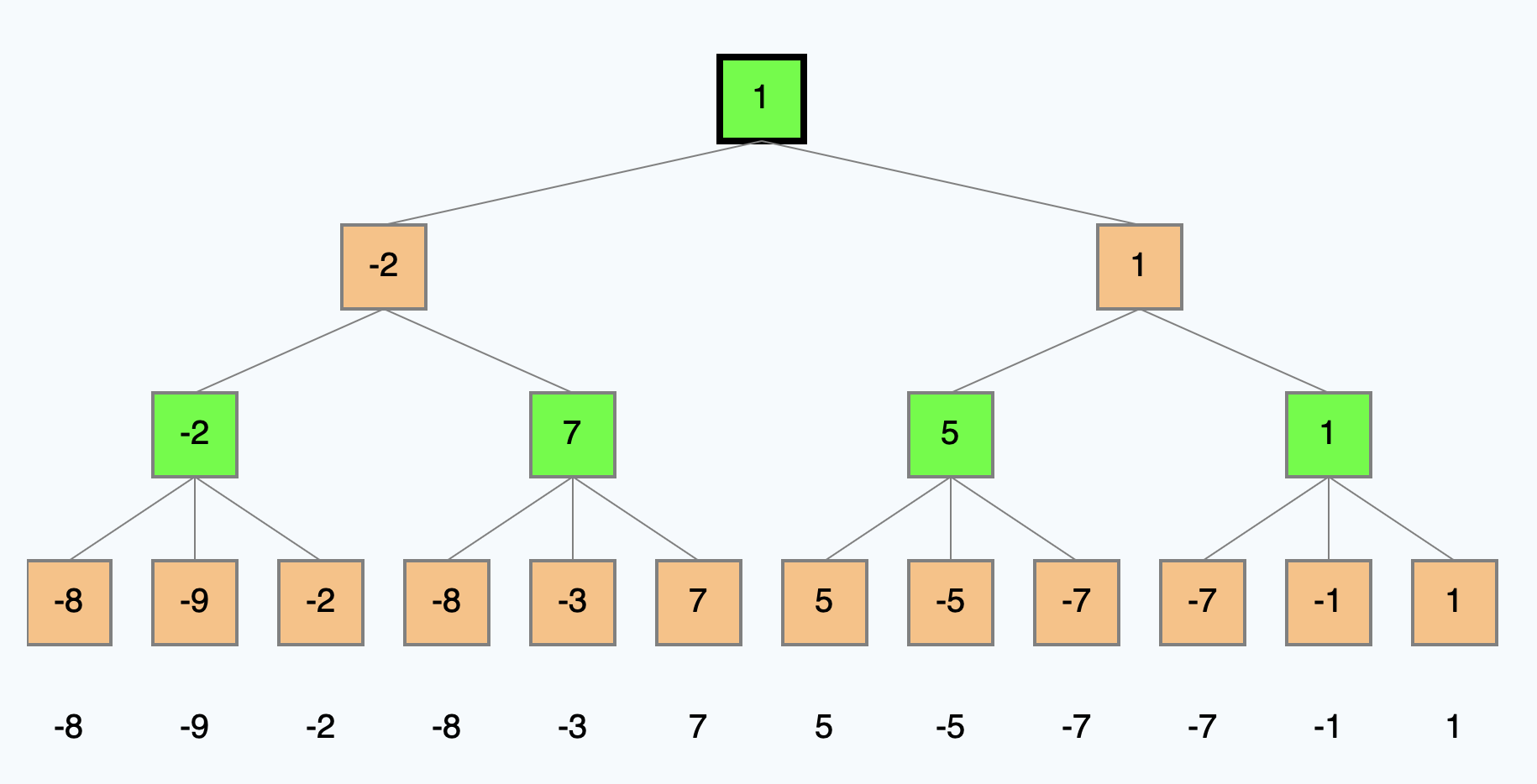
Alpha-Beta-Suche
Die Alpha-Beta-Suche ist eine Optimierung des Minimax-Algorithmus. Die Idee ist, dass gewisse Äste ignoriert werden können, da man weiss, dass sie nicht zu einem besseren Resultat beitragen können.
Implementation
Dazu merkt sich der Algorithmus während der Suche zwei Werte – Alpha und Beta. Diese geben an, welches Ergebnis die Spieler bei optimaler Spielweise laut momentanem Suchstand erzielen können. Mit Hilfe dieser Werte kann entschieden werden, welche Teile des Suchbaumes nicht weiter untersucht werden müssen, weil sie das Ergebnis der Problemlösung nicht beeinflussen können.
Beispiel
Beim untenstehenden Beispiel werden 3 Äste abgeschnitten – diese müssen nicht ausgwertet werden. Dadurch spart man Rechenzeit.
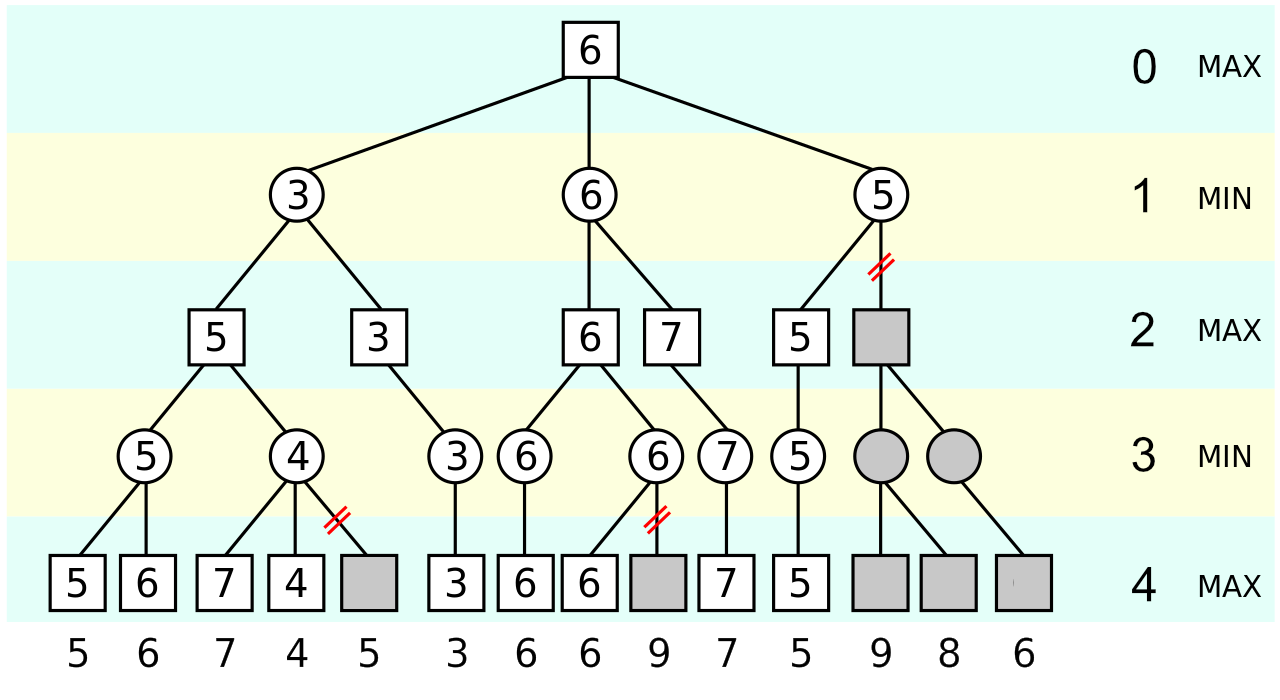
Die ignorierten Äste (pruning) und wieso sie ignoriert werden von links nach rechts:
- kurzer Ast 5
- Da man vom linken Ast (Ebene 3) eine 5 hat und Ebene 3 minimierend ist, spielt es keine Rolle, wenn Ebene 3 unter eine 4 gehen würde! Auf Ebene 5 (maximierend) wird eh die 5 übernommen!
- kurzer Ast 9
- Beide minimierende Äste in Ebene 3 liefern eine 6. Die Ebene 2 übernimmt eine 6, egal ob der rechte Ast eine kleinere Zahl liefern würde.
- langer Ast 8
- Ebene 0 ist maximierend. Die 6 in der Mitte ist der momentan beste Kandidat. Der Ast rechts muss nicht mehr vollständig ausgwertet werden, da auf Ebene 1 höchstens eine 5 kommt und das kleiner ist als die 6.
Aufgabe
Aufgabe: Alpha-Beta
Lösen Sie den Baum mit Hilfe von alpha-beta-pruning. (rot=minimierend, grün=maximierend)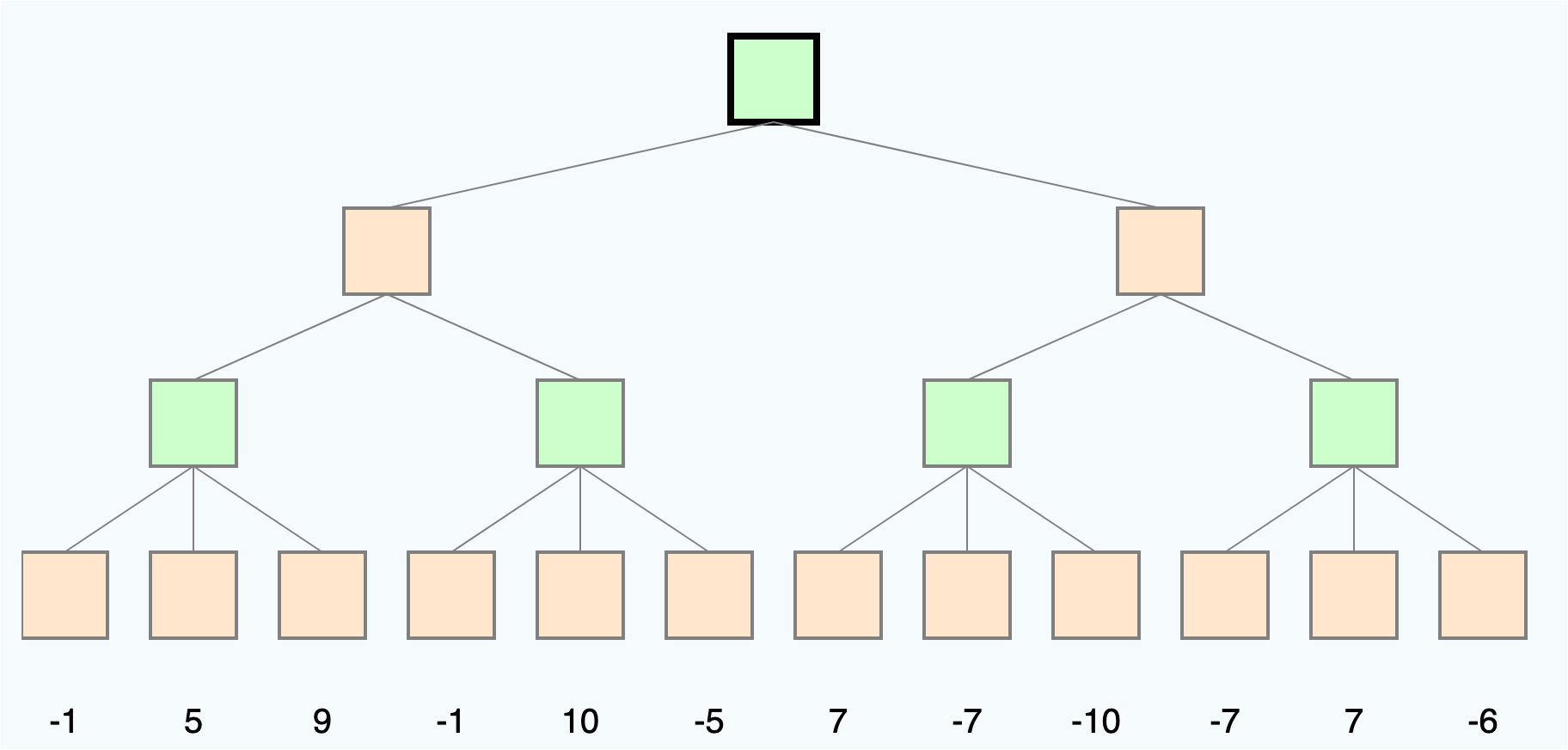
Weitere Beispiele interaktiv lösbar auf:
👉 https://www.yosenspace.com/posts/computer-science-game-trees.html (auf alpha-beta umstellen)
Lösung
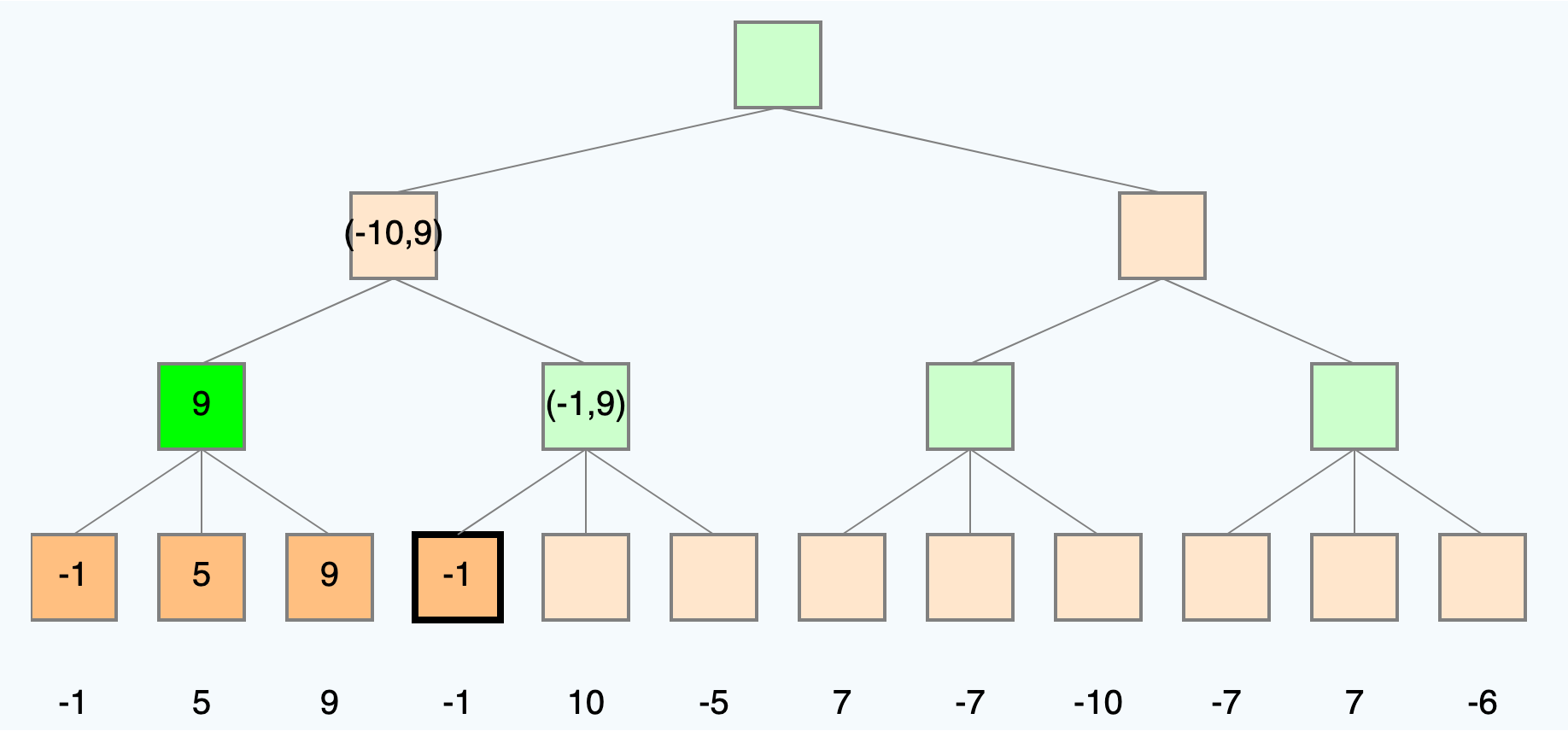
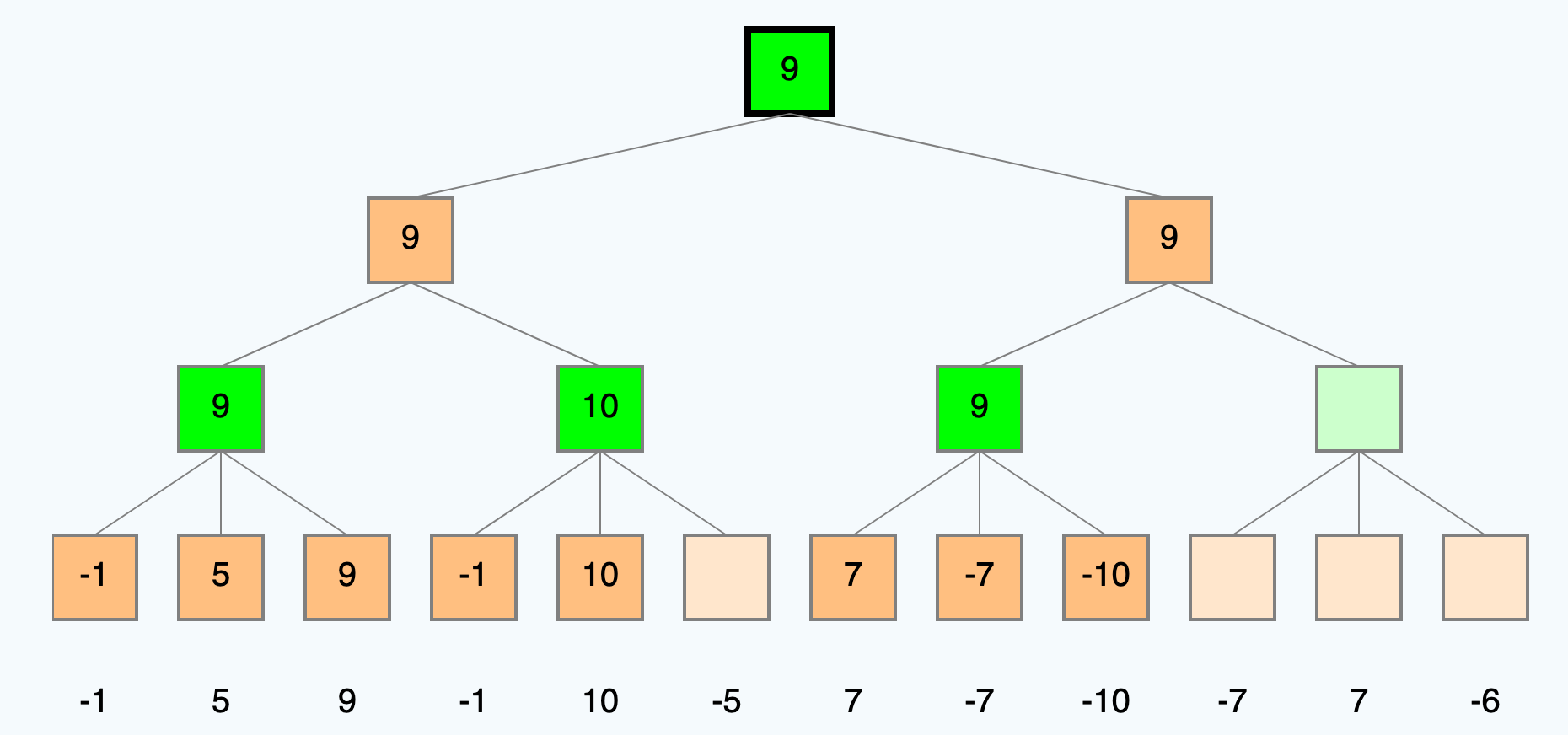
Weitere Quellen
Video
- Algorithms Explained – minimax and alpha-beta pruning (11:00)
- Studyflix – Spieltheorie (deutsche Video-Serie, über Minimax hinaus)