Definition
Ein endlicher Automat ist ein Modell eines Systems mit diskreten Ein- und Ausgaben und einer endlichen Anzahl von Zuständen.
Als Beispiel gucken wir uns eine Lampe mit Schalter an:

Die Lampe hat zwei Zustände: «Licht aus» und «Licht ein». Je nachdem in welchem Zustand sich die Lampe befindet, kann ich durch Drücken des Schalters das Licht ein- oder ausschalten. Das Schalter-Drücken ändert also den Zustand der Lampe. Wir sprechen von einem Zustandsübergang.
Zustandsübergangsdiagramme
Diese Übergänge zwischen den Zuständen kann man in einem Diagramm darstellen:
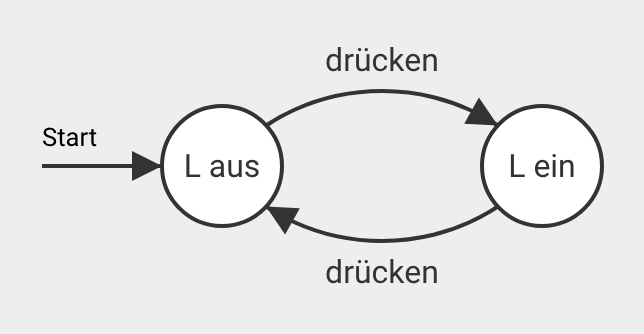
Die Zustände werden durch Kreise gekennzeichnet und benannt. Die Übergänge werden durch benannte Pfeile dargestellt.
Das obige Diagramm lässt sich wie folgt lesen:
Zu Beginn ist das Licht aus. Wenn ich den Schalter drücke, geht das Licht an. Wenn ich den Schalter nochmals drücke, geht es wieder aus.
Übergangstabelle
Dieser Sachverhalt lässt sich auch in einer Tabelle darstellen:
| δ | drücken |
|---|---|
| Licht aus | Licht ein |
| Licht ein | Licht aus |
Die Tabelle wird wie folgt interpretiert:
- Zustände
- Für jeden Zustand gibt es eine Reihe.
- Dessen Name steht in der ersten Spalte (gekennzeichnet durch δ)
- Übergänge
- Für jeden Übergang gibt es eine Spalte
- Der Name des Übergangs steht in der Kopfzeile
- Kann ein Zustand mit diesem Übergang in einen anderen Zustand überführt werden, so steht in der entsprechenden Zeile der neue Zustand. (sonst bleibt der Eintrag leer)
Beispiele und Aufgaben
Getränkeautomat
Ein Getränkeautomat, wie er in der Eingangshalle des Gymers steht, aber etwas vereinfacht:
- akzeptiert nur Ein- und Zweifränkler
- liefert nur Sprite oder Cola
- beides kostet 3.-

Man soll also mit Ein- und Zweifränkler den Automat «füttern». Sobald 3.- erreicht sind, kann man ein Getränk rauslassen.
Wir überlegen uns zuerst welche Zustände und Übergänge es braucht:
- Zustände
- der Automat muss sich den Betrag merken – er soll ja nur bei 3.- ein Getränk rauslassen
- Es gibt also 4 Zustände: 0.-, 1.-, 2.- oder 3.-
Je nachdem wie viel Geld wir reingesteckt haben. - Übergänge
- Je nach Zustand kann man Ein- oder Zweifränkler füttern, oder eine der beiden Getränketasten drücken
Daraus ergibt sich das folgende Übergangsdiagramm:
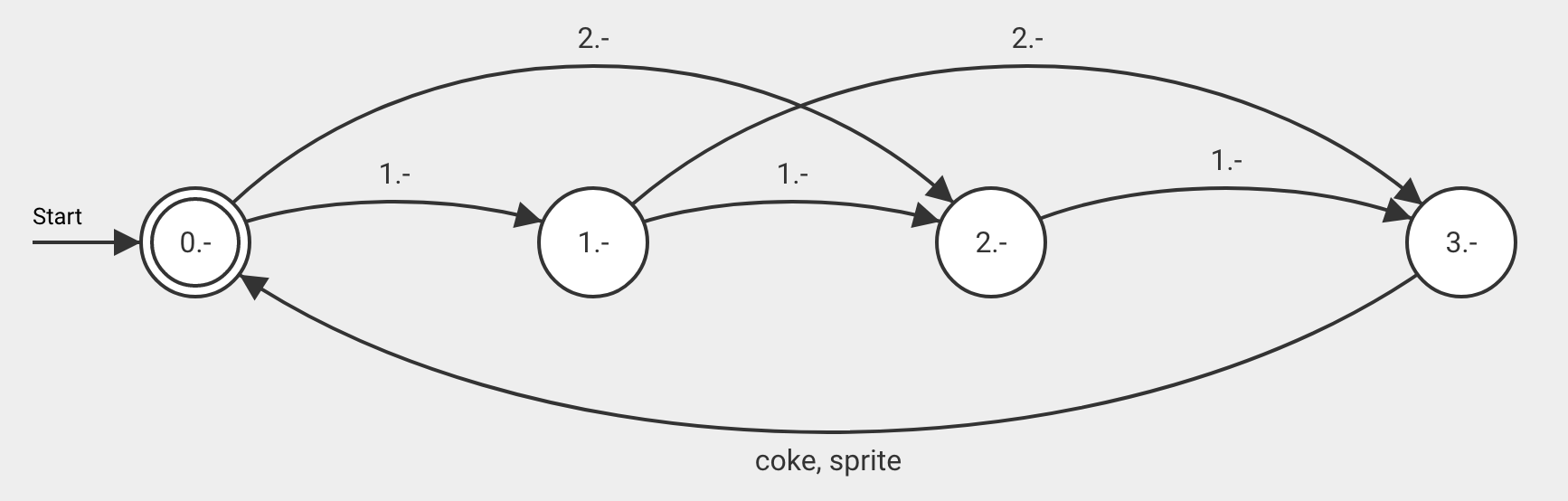
Wir beginnen im Zustand 0.-. Man kann den Automaten mit einem Ein- oder Zweifränkler füttern. So kommt man also in den Zustand 1.- oder 2.-. Nun kann man ihn weiter-füttern, bis der Zustand 3.- erreicht wird. Nur in diesem Zustand reagiert der Automat auf die Getränketaste indem er das Getränk rauslässt und in den End-Zustand 0.- wechselt
| δ | 1.- | 2.- | sprite | coke |
|---|---|---|---|---|
| 0.- | 1.- | 2.- | ||
| 1.- | 2.- | 3.- | ||
| 2.- | 3.- | |||
| 3.- | 0.- | 0.- |
Videogerät
Ein Videogerät kann auch als endlicher Automat angesehen werden:
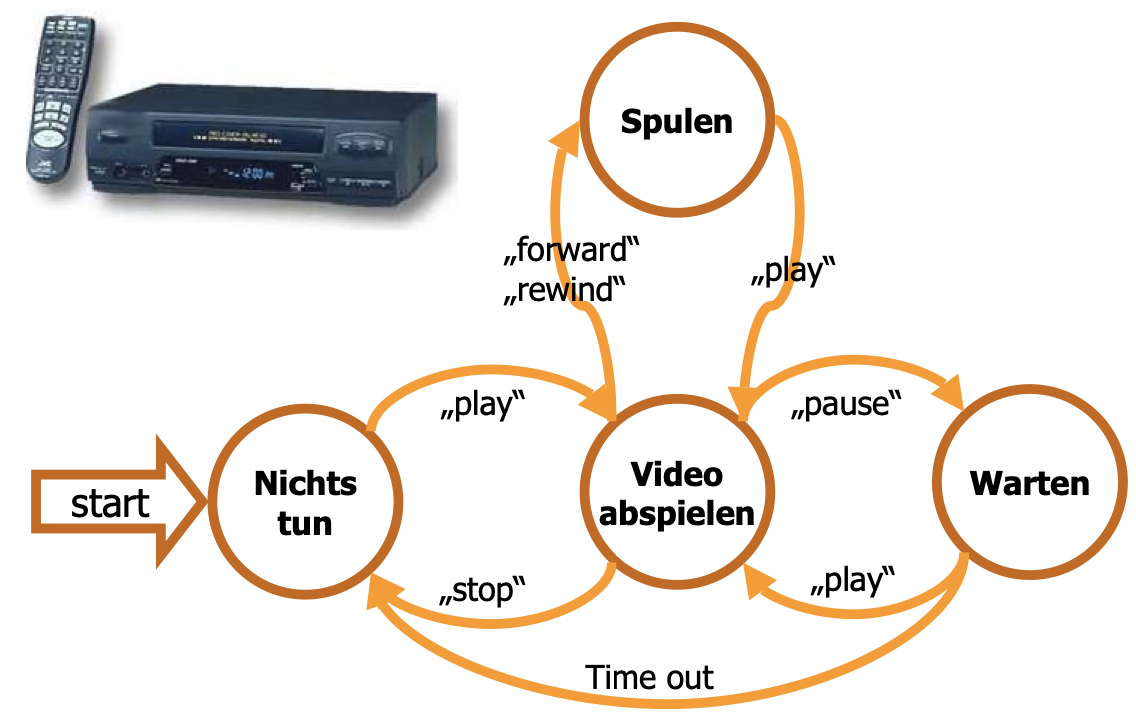
Aufgabe: Videogerät
Erstelle eine Zustandsübergangstabelle für das Videogerät, indem du dir das obenstehende Diagramm liest, genau ansiehst und es dann in eine Tabelle übersetzt.
Lösung: Videogerät
| δ | play | pause | stop | forward | rewind | Time out |
|---|---|---|---|---|---|---|
| Nichtstun | Abspielen | |||||
| Abspielen | Warten | Nichtstun | Spulen | Spulen | ||
| Warten | Abspielen | Nichtstun | ||||
| Spulen | Abspielen |
Ampel
Eine Strassenampel hat 3 farbige Lampen: Rot, Grün und Gelb. Jede Lampe kann ein oder ausgeschaltet werden, was 6 Zustandsübergänge gibt. Die Ampel soll aber nur die folgenden 5 Zustände haben:
- Aus
- ausgeschaltet, nicht in Betrieb
- Gelb
- Achtung, es wird bald rot
- Grün
- alles gut, bitte fahren
- RotGelb
- Motor starten, bald wird es Grün
- Rot
- Stopp
Die Zustände und die möglichen Übergänge sind in der folgenden Tabelle dargestellt:
| δ | grün Aus | grün An | rot Aus | rot An | gelb Aus | gelb An |
|---|---|---|---|---|---|---|
| Aus | Grün | |||||
| Gelb | Rot | Rot | ||||
| Grün | Gelb | Gelb | ||||
| RotGelb | Grün | Grün | Grün | |||
| Rot | RotGelb |
Aufgabe
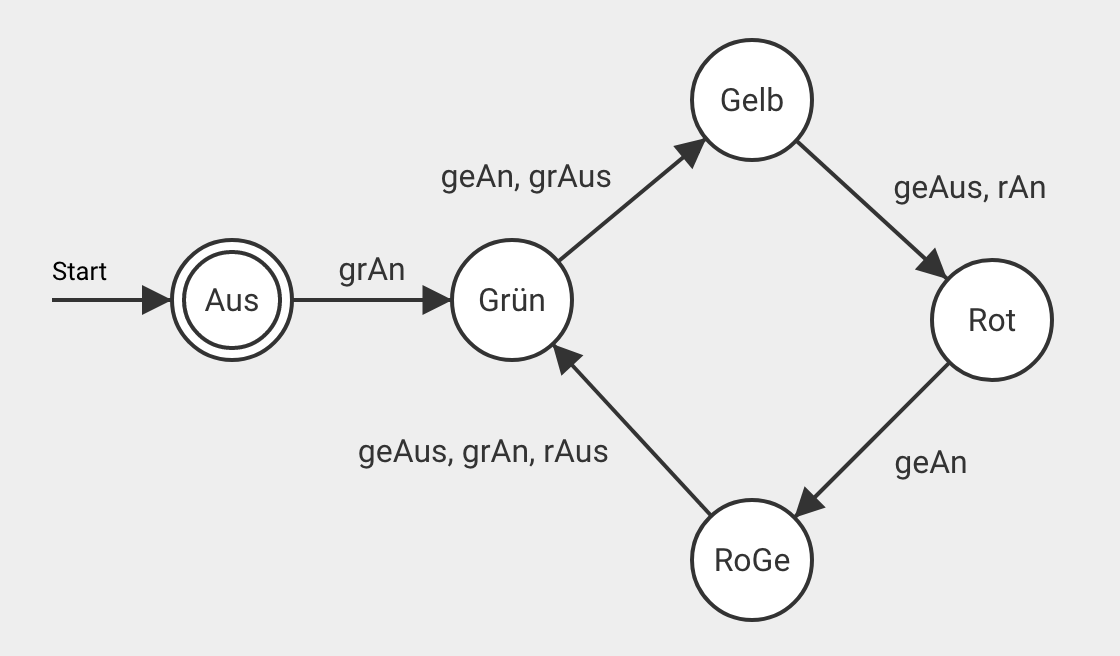
Stelle die Ampel als endlichen Automaten dar, indem du basierend auf der Tabelle ein Zustandsübergangsdiagramm zeichnest.
Lösung: Ampel
weitere
Aufgabe
Erstelle Zustandsübergangsdiagramme und -tabellen für die folgenden beiden Automaten:
- Stoppuhr
- ferngesteuertes Garagentor