A-Stern

Der $A^{\star }$-Algorithmus^[1] (im folgenden $A^{\star }$ genannt) wird verwendet, um in einem Baum oder allgemein in einem Graphen den kürzesten Pfad zwischen zwei Knoten zu finden. Um $A^{\star }$ anwenden zu können, müssen die Kanten mit Kosten versehen sein. Gesucht ist nun der kürzeste (bzw. billigste) Pfad zwischen zwei Knoten.

Bei der Breitensuche wird keine «intelligente» Auswahl der Knoten in der Open-List getroffen, die Knoten werden in willkürlicher Reihenfolge verarbeitet. Der $A^{\star }$ ist eine Verfeinerung dieser Verfahren, wobei folgendermassen immer der vielversprechendste Knoten weiterverarbeitet wird. Es wird abgeschätzt, wie «gut» ein Knoten ist, indem eine Bewertungsfunktion berechnet wird. Die Kosten eines Knotens $N$ beinhalten zwei Beiträge: einerseits die Kosten vom Startknoten bis zu $N$ (wie bei Dijkstra) und andererseits die geschätzten Kosten von $N$ bis zum Zielknoten. Diese Bewertungsfunktion $f(N)$ für einen Knoten $N$ wird also folgendermassen definiert:

Definition

$$f(N)=g(N)+h(N)$$

wobei $g(N)$ die Kosten des Pfades vom Startknoten zu $N$ darstellt und $h(N)$ die geschätzten Kosten eines optimalen Pfades von $N$ zum Zielknoten darstellt.

Bei der Schätzung muss gelten:

$$h(N)\ge h^{\star }(N)$$

wobei $h^{\star }(N)$ die wirklichen Kosten des optimalen Pfades von $N$ zum Zielknoten sind.

Dabei ist $h$ normalerweise unbekannt und kann nur abgeschätzt werden. Dazu muss gelten: $h(N)\ge h^{\star }(N)$, wobei $h^{\star }(N)$ die wirklichen Kosten des optimalen Pfades von $N$ zu einem Zielknoten sind. Das heisst $h$ darf die Kosten eines Knotens nie überschätzen. Oft wird z.B. die euklidische Distanz zum Ziel verwendet.

Die Funktion $h$ ist eine sog. Heuristik, also eine Abschätzung des wahren Werts. So kann die Suche nach dem optimalen Pfad oft wesentlich beschleunigt werden, was beim $A^{\star }$ ausgenutzt wird. Man kann zeigen, dass der $A^{\star }$ immer den kürzesten Weg findet, wenn es einen gibt.

Beispiel

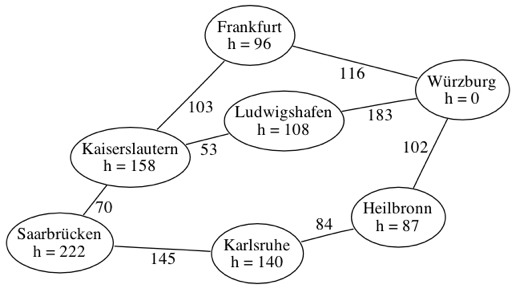
Wir suchen den schnellsten Weg von Würzburg nach Saarbrücken. Durch Abstraktion der Karte haben wir den folgenden gewichteten Graphen erhalten. Zusätzlich kennen wir für jeden Knoten eine Heuristik, nämlich die Distanz der Luftlinie nach Würzburg:

Karte	Aktion
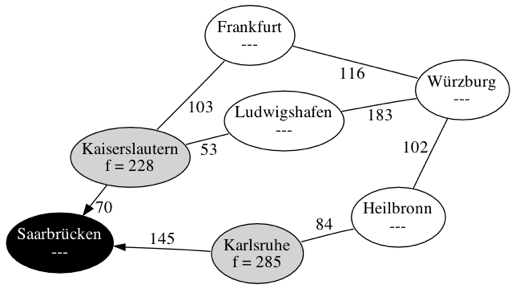
Schritt 1
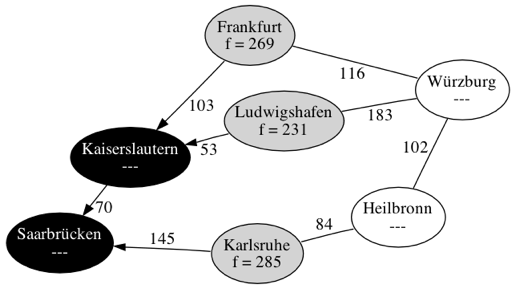
Schritt 2
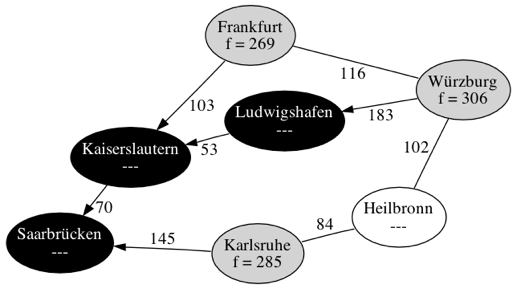
Schritt 3
Schritt 4
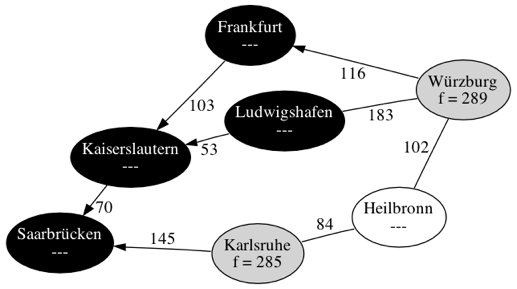Schritt 5
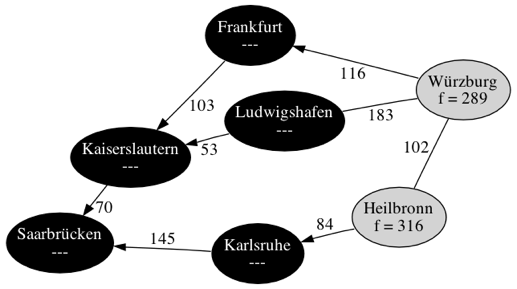Schritt 6

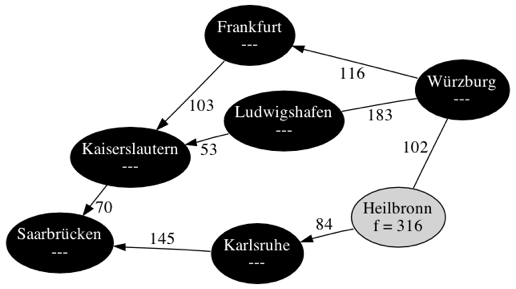Aufgabe: Schiebepuzzle 1

Beim Spiel «8-Puzzle» geht es darum, von einer beliebig durcheinander gebrachten Position der Zahlen durch Verschieben einzelner Zahlen in das jeweils leere Feld die folgende Zielposition zu erreichen:

Puzzle Zielposition

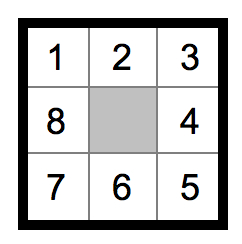
Der $A^{\star }$-Algorithmus kann verwendet werden, um diese Aufgabe für beliebige Ausgangsstellungen zu lösen. Im Folgenden geht es darum, diesen algorithmischen Lösungsweg nachzuvollziehen und mit Suchverfahren ohne Heuristik zu vergleichen.

Puzzle Ausgangsposition

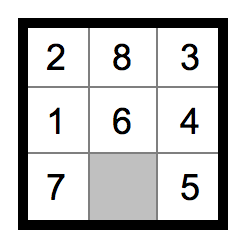
1. Finde mittels einer Tiefensuche (maximale Tiefe: 6) den Lösungsweg zur beschriebenen Zielposition aus der dargestellten Ausgangsstellung.
   Vervollständige dazu den Suchbaum auf dem Zusatzblatt von links nach rechts bis der Zielknoten erreicht ist. Schreibe neben jeden Knoten die Reihenfolge, in welcher diese besucht werden (z.B. mit roter Farbe)

Vorlage 1 (pdf)

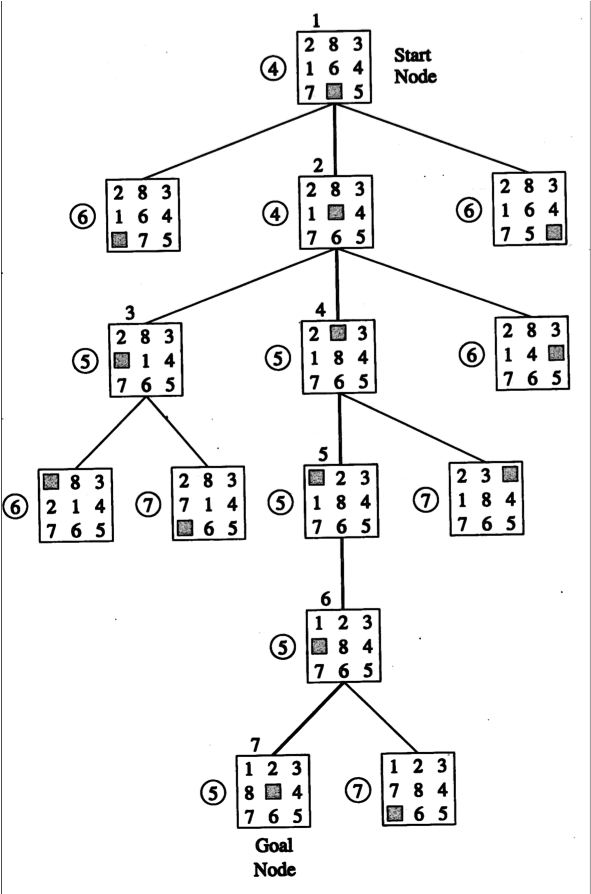
Lösung

Aufgabe: Schiebepuzzle

2. Denke dir eine Heuristik aus (d.h. definiere die Funktion $h(N)$), um dieses Problem mit dem $A^{\star }$ zu lösen. Diese Heuristik soll ein Mass dafür sein, wie nahe am Ziel der jeweilige Knoten ist.

Lösung

h(N) := Anzahl falsch platzierte Zahlen

Diese Heuristik erfüllt die Bedingungen: Jede falsch platzierte Zahl muss in mindestens einem Zug verschoben werden, um an den korrekten Ort zu kommen.

Aufgabe: Schiebepuzzle

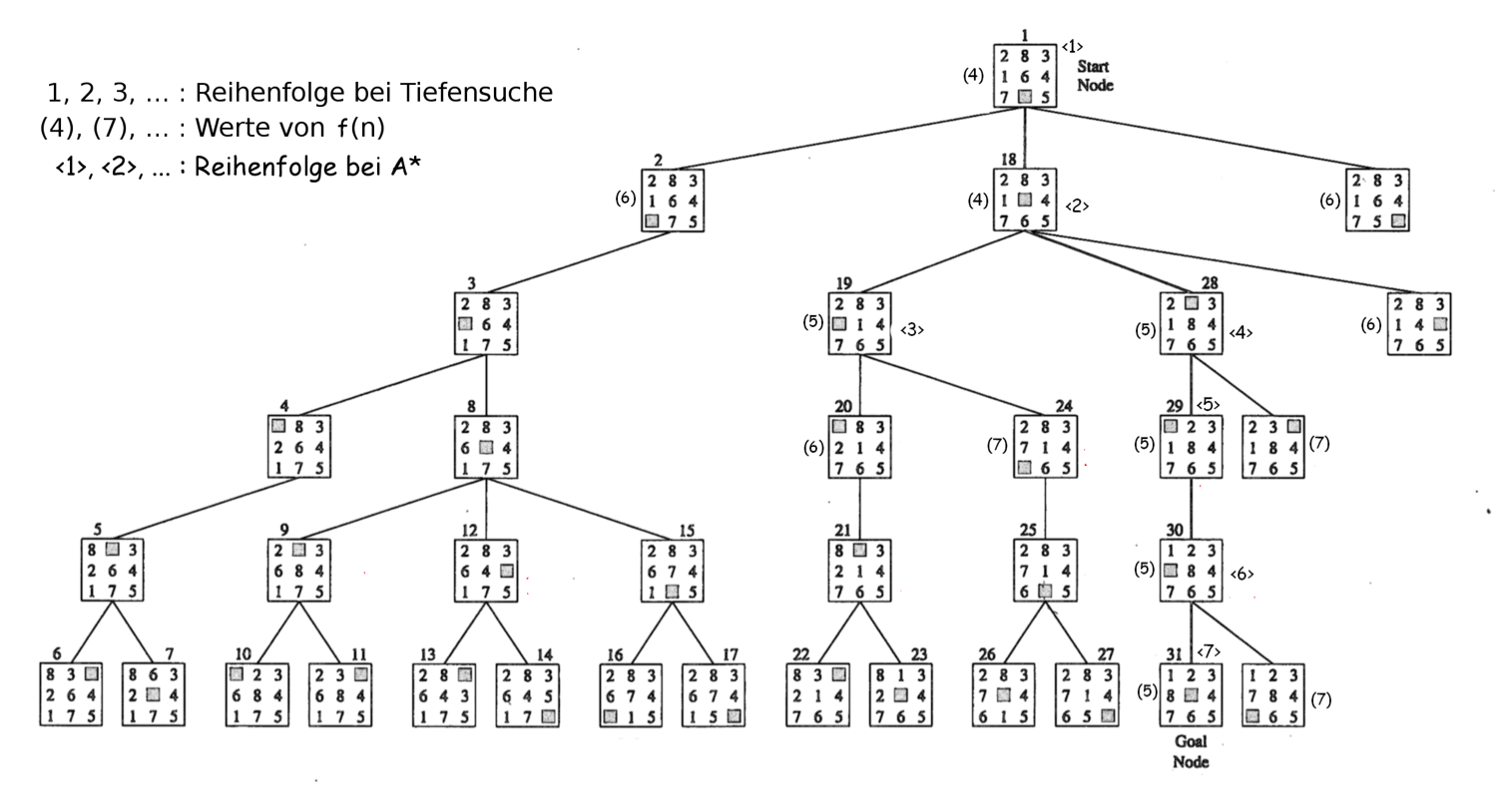
3. Zeichne in den Suchbaum aus Aufgabe 1 ein, wie der $A^{\star }$ mit deiner Funktion $h(N)$ von Aufgabe 2 den Baum absuchen würde. Beginne beim Startknoten und berechne für alle Nachfolgeknoten
   $f(n)=g(n)+h(n)$. Dabei ist $g(n)$ die Anzahl bereits zurückgelegten Kanten. Verfolge immer denjenigen Nachfolgeknoten weiter, der den kleinsten Wert von $f(n)$ hat. Schreibe neben jeden betrachteten Knoten den Wert der Funktion $f(N)$ (z.B. so: (1) mit grün) und die Reihenfolge in welcher die Knoten besucht werden (z.B. <4> mit blau).
   Ist der $A^{\star }$ schneller als die Tiefensuche ohne Heuristik? Wie viele Knoten müssen besucht werden? Vergleiche diese Zahl mit denjenigen der Breiten- bzw. Tiefensuche.

Vorlage 2 (pdf)

Lösung

Der Algorithmus ist bedeutend schneller als ohne Heuristik. Es müssen nur 7 Knoten expandiert werden, bei der Breitensuche waren es 34, bei der Tiefensuche 31 (diese Zahl ist aber abhängig davon, wie man den Baum zeichnet).

$A^{\star }$-Algorithmus in Pseudocode

program a-star
   OPEN.add(startNode)
   repeat
      bestNode := OPEN.remove(Node with minimal f-Value)
      if (bestNode == targetNode) then return bestNode
      calcF(bestNode.successors())
      OPEN.add(bestNode.successors())
      CLOSED.add(bestNode)
   until (OPEN.isEmpty)
   return no path found
end

Vergleich

Abschliessend wollen wir die 3 Algorithmen miteinander vergleichen:

	Breitensuche	Dijkstra	A-Stern
Ansatz	«Brute Force»	«Algorithmisch»	«Heuristisch»
Voraussetzung	normaler Graph	gewichteter Graph	gewichteter Graph inkl. Heuristik

Aufgabe

Auf der verlinkten Seite kannst du Breitensuche, Dijkstra und A-Stern miteinander vergleichen. Teste die Seite aus und beantworte folgende Fragen:

• Was ist «Breadth First»?
• Was ist «Depth First»?
• Wofür stehen die Farben wenn man bei Terrain den Eintrag Simplex Terrain wählt. Welchen Einfluss haben diese auf den A-Stern-Algorithmus?

pathfindout.com

Zusatzaufgabe

Der A-Stern-Algorithmus kommt auch in Computer-Spielen zu Einsatz:
Lies dich durch den folgenden Beitrag durch und teste die tollen (und teilweise interaktiven) Visualisierungen:

www.redblobgames.com

---

1. Teile übernommen von Ryter, M.: Einführung in die künstliche Intelligenz. http://www.swisseduc.ch/informatik/theoretische_informatik/kuenstliche_intelligenz/ (26.12.2009) ↩︎