Einleitung
Die Spieltheorie ist ein Zweig der Mathematik. Es geht dabei um Strategien, deren Erfolg nicht nur vom eigenen Handeln, sondern auch von Aktionen anderer abhängt.
Spieltheorie wird in den Wirtschaft-, Rechts- und Politikwissenschaften, aber auch in der Psychologie, Soziologie und Biologie eingesetzt.
In der Informatik, können die Algorithmen der Spieltheorie implementiert werden. Z.B. um einen Computergegner im Tic-tac-toe oder im Schach zu erstellen.
Arbeits-Auftrag
Aufgabe
Verschaffe dir mit den verlinkten Videos und Beiträgen eine Übersicht zum Thema «Spieltheorie» – im speziellen zum Minimax- und Alpha-Beta-Algorithmus.
Teste anschliessend deinen Fortschritt an Hand der Selbsttest welche du zuunterst auf dieser Seite findest.
Links zu Minimax und Alpha-Beta
Video
- Algorithms Explained – minimax and alpha-beta pruning (11:00)
- Studyflix – Spieltheorie (deutsche Video-Serie, über Minimax hinaus)
Artikel
Wikipedia
Interaktiv
Schach
- Sind Schachspieler intelligenter?
- Was machen gute Schachspieler anders als Amateure?
- Coding Adventure: Chess AI
Selbsttests
Selbsttest 1
Aufgabe
Erklären Sie, wie die Werte der einzelnen Knoten zustande kommen. 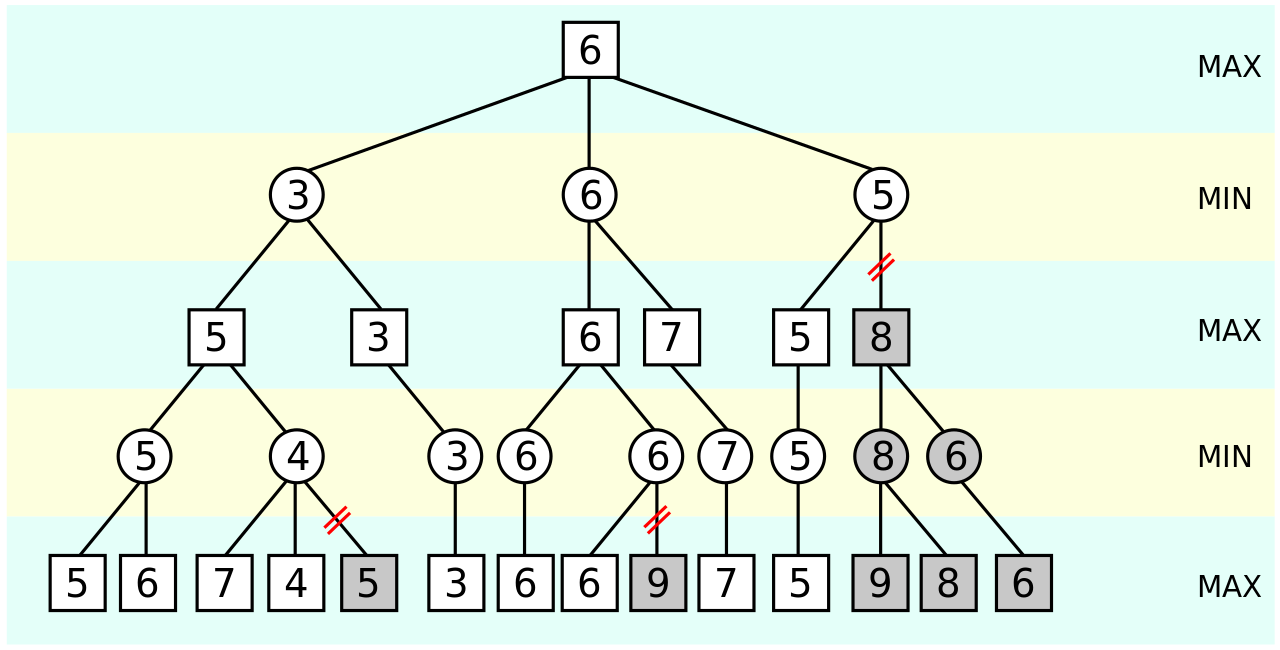
Lösung
Minimax-Algorithmus:
Die Quadrate stellen die Züge der Spieler im Algorithmus dar (Maximierung), die Kreise die Züge der Gegner (Minimierung). Die Werte in den Quadraten und Kreisen stellen den Wert α des Minimax-Algorithmus dar. Die untersten Knoten sind entweder durch die Endstellung (Sieg oder Niederlage) oder durch eine Stellungsbewertung gegeben.
Alpa-Beta-Suche:
Der Minimax-Algorithmus durchsucht für die Auswahl alle Knoten vollständig und benötigt somit viel Zeit. Die Alpha-Beta-Suche hingegen durchsucht zunächst nur den ersten Knoten vollständig nach minimalem Wert. In allen weiteren Knoten wird nur solange gesucht, bis der Wert dieses Minimum erreicht oder unterschreitet. Dann steht fest, dass dieser Knoten für den ersten Spieler nicht besser als die erste ist, und die Suche darin kann abgebrochen werden. Andernfalls ist dieser Knoten eine bessere Wahl, und ihr minimaler Wert dient für die weitere Suche als neue Grenze.
Selbsttest 2
Aufgabe
Erklären Sie, wie die Werte der einzelnen Knoten zustande kommen.
Selbsttest 3
Aufgabe
Lösen Sie den Baum mit Hilfe von alpha-beta-pruning.
Lösung
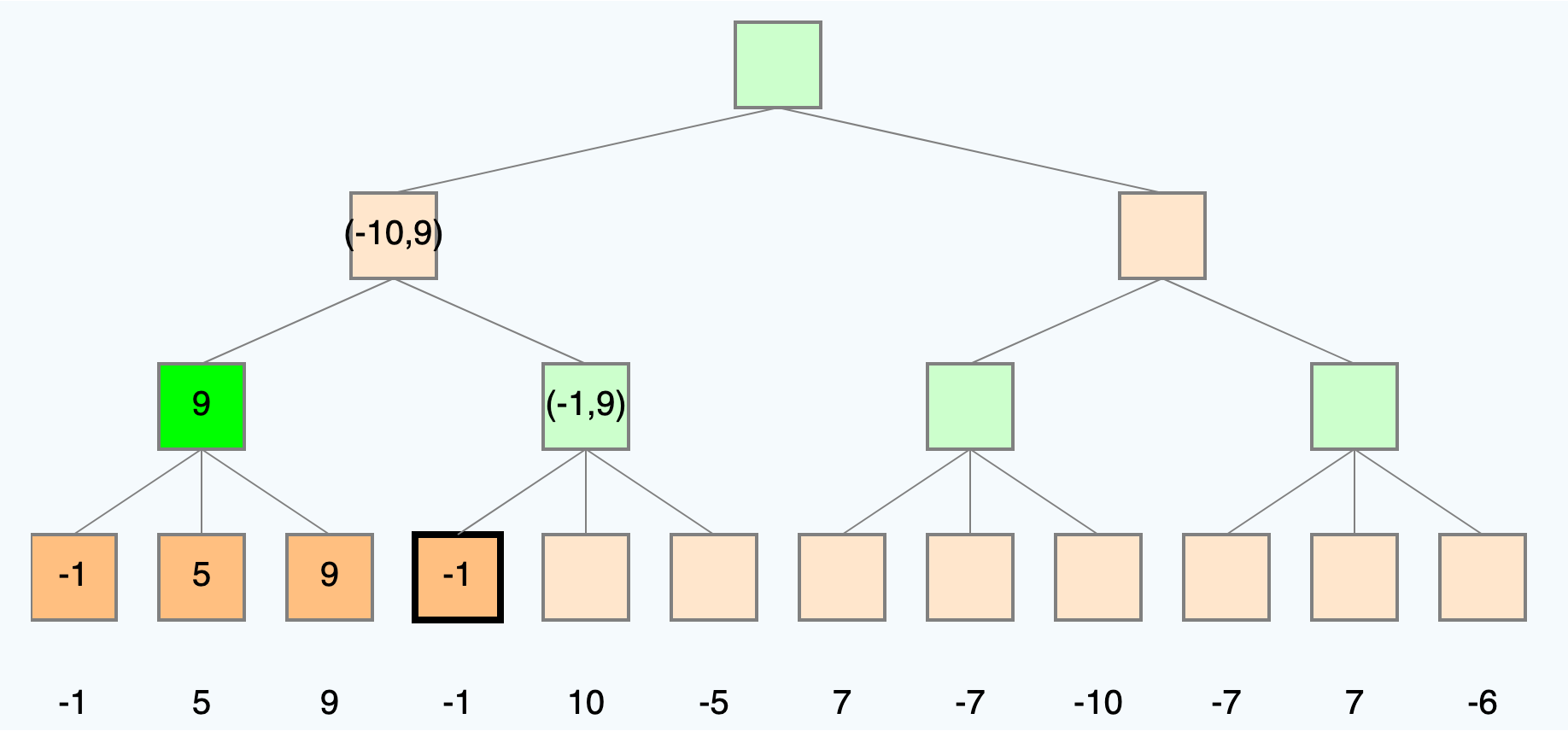

Weitere Beispiele interaktiv lösbar auf:
👉 https://www.yosenspace.com/posts/computer-science-game-trees.html
Zusatzaufgabe
Zusatzaufgabe
- Überfliegen Sie das (ausführliche) Video, so dass sie es begriffen haben.
- Programmieren Sie die gezeigte Lösung in Python!
👉 Coding Challenge: Tic-tac-toe AI with Minimax Algorithm (26:32)
