Ihr bearbeitet in Zweierteams von den nachfolgenden 5 Posten so viele wie möglich. Macht euch zu jedem Posten Notizen, so dass wir anschliessend die Erkenntnisse der einzelnen Teams im Plenum zusammentragen können. Damit nicht alle die Posten in der gleichen Reihenfolge durchgehen, könnt ihr hier Würfeln:
# Posten 1 – Zeichnen
Wir beschreiben eine ganz einfache Zeichnung mit Text. Aus dem Text versuchen wir dann wieder die Zeichnung zu erhalten. Wie gut klappt das? Auf was muss man man achten?
Zeichnung beschreiben
- hole bei der Lehrkraft eine Vorlage ab
- schaue dass die Teampartnerin/der Teampartner die Vorlage nicht sieht
- beschreibe das Bild so exakt wie möglich unterhalb des Falzstrichs
- falte das Blatt beim Falzstrich und lege es so, dass die Zeichnung auf der Rückseite liegt und verdeckt ist
Nun tauscht ihr im Zweierteam die Blätter aus.
Beschrieb umsetzen
- nimm ein leeres Blatt Häuschenpapier
- nimm die Beschreibung deiner Teampartnerin/deines Teampartners, ohne dass du die Zeichnung auf der Rückseite siehst
- versuche an Hand der Beschreibung die Zeichnung zu rekonstruieren
- vergleiche am Schluss dein Ergebnis mit dem Original auf der Rückseite
Besprechung im Team
Besprecht euch im Zweierteam und hält folgendes fest:
- Was hat geklappt und wieso?
- Was hat nicht geklappt und wieso nicht?
# Posten 2 – Papierflieger
Mit Hilfe einer illustrierten Anleitung lässt sich einfach ein Papierflieger falten.
Border
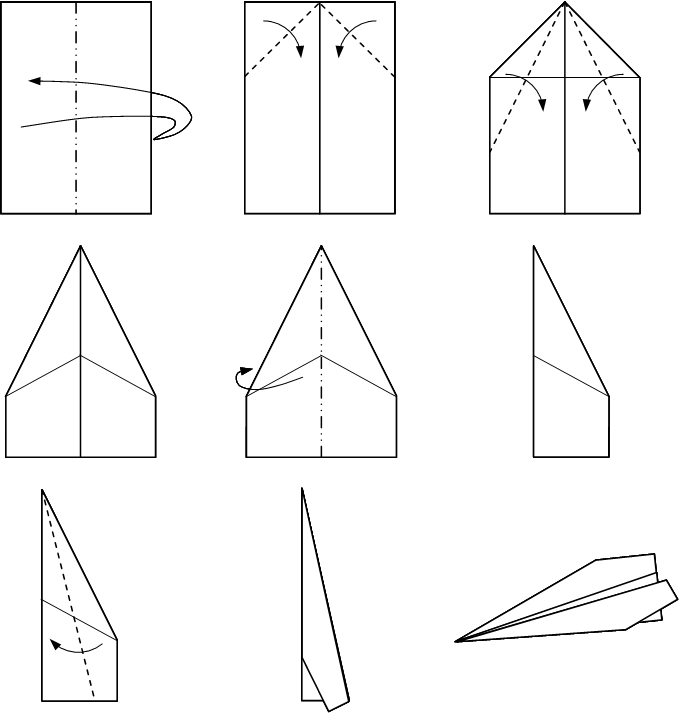
«Rakete» falten
- Nimm ein Blatt Papier.
- Versuche gemäss Faltanweisung so exakt wie möglich eine «Rakete» zu falten.
- Vergleicht im Zweierteam euer Endprodukt.
Border

«World Record»
Obenstehend findet ihr eine Anleitung für einen Weltrekord-Papierflieger. (Diesen müsst ihr nicht falten!)
Vergleicht diese Anleitung mit der ersten:
- Welche Gemeinsamkeiten findet ihr?
- Worin unterscheiden sich die Anleitungen?
- Welche Unterschiede haben wirklich Auswirkungen auf die auszuführenden Anweisungen?
# Posten 3 – Kochrezept
Wir schauen uns das folgende Rezept an:
Border

Zutaten
- Berechne die Zutatenmengen, falls für alle im Raum anwesende gekocht werden soll.
- Kannst du die Zutatenmengen mit einer Formel notieren, so dass für eine beliebige Personenzahl einfach die korrekte Menge berechnet werden kann.
# Posten 4 – Musik
In der Notenschrift verwendet man Wiederholungszeichen (opens new window), damit man nicht nochmal das selbe aufschreiben muss.
Wir schauen uns die folgenden Noten an:
Wiederholung
Bestimme die folgenden Werte:
- Anzahl notierte Takte auf dem Blatt
- Anzahl gespielte Takte (inkl. Wiederholungen)
Berechne nun das Verhältnis:
Was sagt dieses Verhältnis über das Musikstück, resp. die Notation aus?
Hinweis
Du kannst dein Ergebnis überprüfen indem du das Lied abspielst:
https://musescore.com/user/27687306/scores/4913846 (opens new window)
# Posten 5 – Geburtstag
Um verschiedene Anweisungen in einer bestimmten Reihenfolge zu notieren, kann man ein sogenanntes Flussdiagramme (in der Informatik auch Programmablaufplan) verwenden. Dabei werden verschiedene einzelne Aktionen mit Pfeilen verbunden. Es sind auch Verzweigungen möglich.
Hier stehen z.B. Anweisungen wie man zu einem bestimmten Datum gegeben aus Tag, Monat und Jahr, den Wochentag herausfinden kann:

Datum
- Führt den obenstehenden Programmablaufplan 2x aus
- Als Datum wählt ihr eure Geburtsdaten
- Stimmt das Ergebnis? (Wisst ihr an welchem Wochentag ihr geboren wurdet? Wenn nicht, wie könnte man das überprüfen?)
# Ergebnisse Gruppenarbeit
Border
- eindeutige Beschreibung, sei es mit Text, Bildern oder Symbolen (z.B. Kochrezept mit Text oder grafische Falzanleitung)
- besteht aus einzelnen, kleinen und klaren Schritte (z.B. Falzanleitungs-Schritt, Flussdiagramm-Element, Kochschritt)
- für identische Eingaben kommt immer das selbe raus (z.B. bei gleichem Geburtsdatum kommt der gleiche Wochentag raus, wenn beide die Falzanleitung exakt befolgen kommt derselbe Flieger raus)
- Strukturen wie Wiederholung (z.B. Kochanweisung) oder Verzweigungen (z.B. Flussdiagramm)
- kommt immer an ein Ende (keine endlose Wiederholung)
- löst ein Problem oder eine «Klasse» von Problemen (z.B. Kochrezept: für 4 Personen oder für 12 Personen, oder nur für eine Person: Mengenangaben umrechnen, Schritte bleiben gleich, Wiederholungen passen sich auch an.)


