Wir erforschen die Komplexität am Beispiel der Suche: Gegeben sei eine Liste mit Namen.

liste = ["Finn", "Geremia", "Gian", "Janis", "Kenneth", "Max", "Pascal", "Philipp", "Roman", "Samantha", "Vincent"]

Es gibt nun «intelligente» und «weniger intelligente» Möglichkeiten, diese Liste nach einem bestimmten Element zu durchsuchen.

Lineare Suche #

Wir gehen die Liste Element um Element durch und vergleichen die Elemente mit dem gesuchten Element:

def search1(liste, search_item):
    i = 1
    for item in liste:
        if item == search_item:
            return i
        i = i + 1

Wir zählen wie viele Elemente wir vergleichen müssen und geben diese Zahl aus.

Der beste Fall wäre die Suche nach «Finn» – hier können wir gleich beim ersten Element die Suche abbrechen.

Der schlechteste Fall wäre die Suche nach «Vincent» – hier müssen wir alle Elemente durchgehen und werden erst beim letzten fündig. (oder gleich schlecht: die Suche nach einem Namen der gar nicht vorkommt!)

Im Durchschnitt werden wir in der Hälfte der Liste fündig!

Uns interessiert aber der schlechteste Fall! – Wenn ein Programm im Schnitt einige Sekunden benötigt, aber dann im schlechtesten Fall trotzdem ein Jahr, ist es nicht wirklich brauchbar!

Komplexität #

Was ist nun, wenn wir die Liste verlängern? Dann steigt die Anzahl der Vergleiche natürlich auch: Für eine doppelt so lange Liste müssen wir auch doppelt so viele Vergleiche anstellen.

Wir haben hier also ein lineares Wachstum, welches wir in der sogenannten O-Notation wie folgt schreiben:

Binäre Suche #

Eine «intelligentere Suche» macht sich zu Nutze, dass diese Liste alphabetisch sortiert ist. Wir vergleichen unser gesuchtes Element mit dem Element in der Mitte der Liste. Kommt unser gesuchtes Element im Alphabet nach dem Element in der Mitte, so halbieren wir die Liste und gucken uns nun nur noch den zweiten Teil an. Dort wiederholen wir das Prozedere, bis wir das Element finden.

Dadurch entsteht ein binärer Baum:

«Max» ist genau in der Mitte, «Gian» und «Roman» sind in der Mitte der beiden Hälften, usw.
Mit jedem Vergleich halbieren wir also die Menge der in Frage kommenden Elemente.

Wir kommen in diesem Beispiel in maximal 4 Schritten zu unserem Ziel. (Der Baum hat 4 Ebenen)

Komplexität #

Da die Liste nach jedem Aufruf halbiert wird, haben wir nach dem ersten Teilen noch $n/2$ Elemente, nach dem zweiten Schritt $n/4$ Elemente, nach dem dritten Schritt $n/8$ Elemente, usw. Daher lässt sich allgemein sagen, dass im i-ten Schritt maximal $n/2^i$ Elemente übrigbleiben. Das ergibt $lo{g}_{2}n$ Vergleiche bei der Suche.

Diese Suche hat also kein lineares Verhalten mehr, sondern ein logarithmisches. Wir notieren das in der O-Notation wie folgt:

Die binäre Suche ist also schneller als die lineare. Gerade bei längeren Listen macht sich das sehr stark bemerkbar:

Code #

Eine Möglichkeit, die binäre Suche zu implementieren, sieht wie folgt aus:

def search2(liste, search_item):
    i = 1
    min = 0
    max = len(liste)
    index = (max - min) // 2
    while True:
        item = liste[index]
        if item == search_item:
            return i
        elif item < search_item:
            min = index
        else:
            max = index
        index = min + (max - min) // 2
        i = i + 1

Es wird immer nur ein Teil der Liste durchsucht, der nach jedem Schritt kleiner wird. Der Teil der Liste wird durch die Variablen min und max eingegrenzt.

experimenteller Vergleich #

Direkt-Vergleich für eine Liste #

Wir wählen 10000 Mal zufällig ein Element der Liste aus und schauen wie viele Schritte die beiden Suchalgorithmen brauchen, um es zu finden. Den Durchschnitt geben wir aus.

import random

def test1():
    i = 0
    count1 = 0
    count2 = 0
    while i < 10000:
        item = liste[random.randint(0, len(liste) - 1)]
        count1 = count1 + search1(liste, item)
        count2 = count2 + search2(liste, item)
        i = i + 1
    print("search 1: ", count1 / i)
    print("search 2: ", count2 / i)

Vergleich bei Zunahme der Listenlänge #

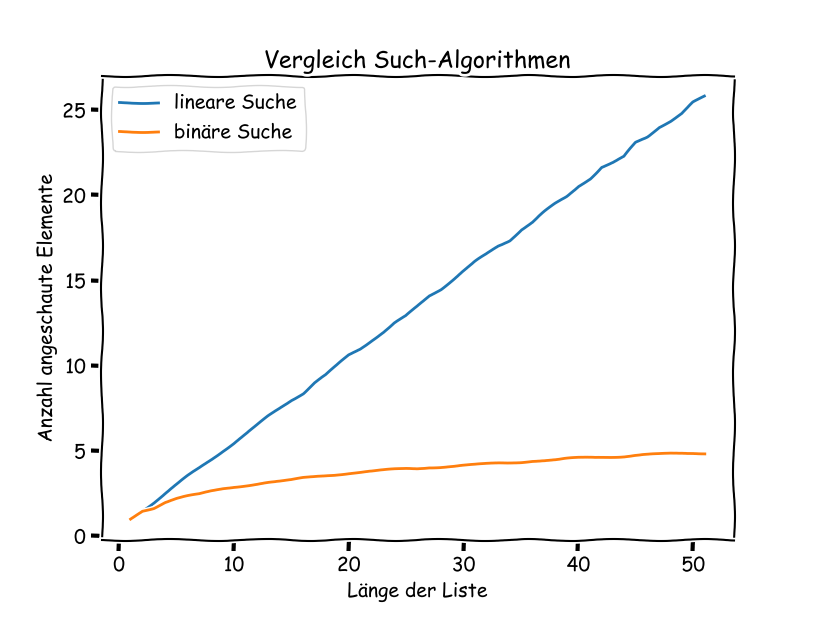
Wir führen denselben Vergleich nun für Listen mit unterschiedlicher Länge aus: Die äussere while-Schleife sorgt dafür, dass aus der ursprünglichen Liste, unterschiedlich lange Unterlisten erstellt werden. Dazu wird die Liste «zerschnitten» mit liste[0:x]. Diese Unterliste wird immer länger, bis wir dann die Original-Liste wieder erhalten. Für jede Unterliste wird wiederum der Durchschnitt von 10000 Suchen eines zufälligen Elementes berechnet.

import matplotlib.pyplot as plt

def test2():
    plot_x = []
    plot_y1 = []
    plot_y2 = []

    x = 1
    while x < len(liste):
        short_liste = liste[0:x]
        i = 0
        count1 = 0
        count2 = 0
        while i < 10000:
            item = liste[random.randint(0, len(short_liste) - 1)]
            count1 = count1 + search1(short_liste, item)
            count2 = count2 + search2(short_liste, item)
            i = i + 1

        plot_x.append(x)
        plot_y1.append(count1 / i)
        plot_y2.append(count2 / i)
        x = x + 1
        
    plt.plot(plot_x, plot_y1, plot_y2)
    plt.show() 

Am Schluss sind in den Variablen plot_x, plot_y1 und plot_y2 die Ergebnisse abgespeichert. Diese können nun z.B. mit der matplotlib ausgegeben werden.

Für eine Liste bis Länge 50 führt dies zu folgendem Output:

Theorie #

Algorithmen mit einer polynomialen Laufzeit von $n^2$ oder allgemein $n^k$ skalieren bereits schlecht. Das bedeutet, dass sie bei einem grösseren Input, kaum brauchbar sind, weil sie das Resultat nicht mehr in nützlicher Zeit liefern können. Sie gelten aber immer noch als effizient. Man muss die Input-Länge kontrollieren.
Algorithmen mit exponentieller Laufzeit, also $2^n$ oder $k^n$ , werden nicht mehr als effizient bezeichnet. Ihre Komplexität wächst so stark mit steigendem Input, dass sehr bald schon keine Resultate mit vernünftigem Aufwand möglich sind.

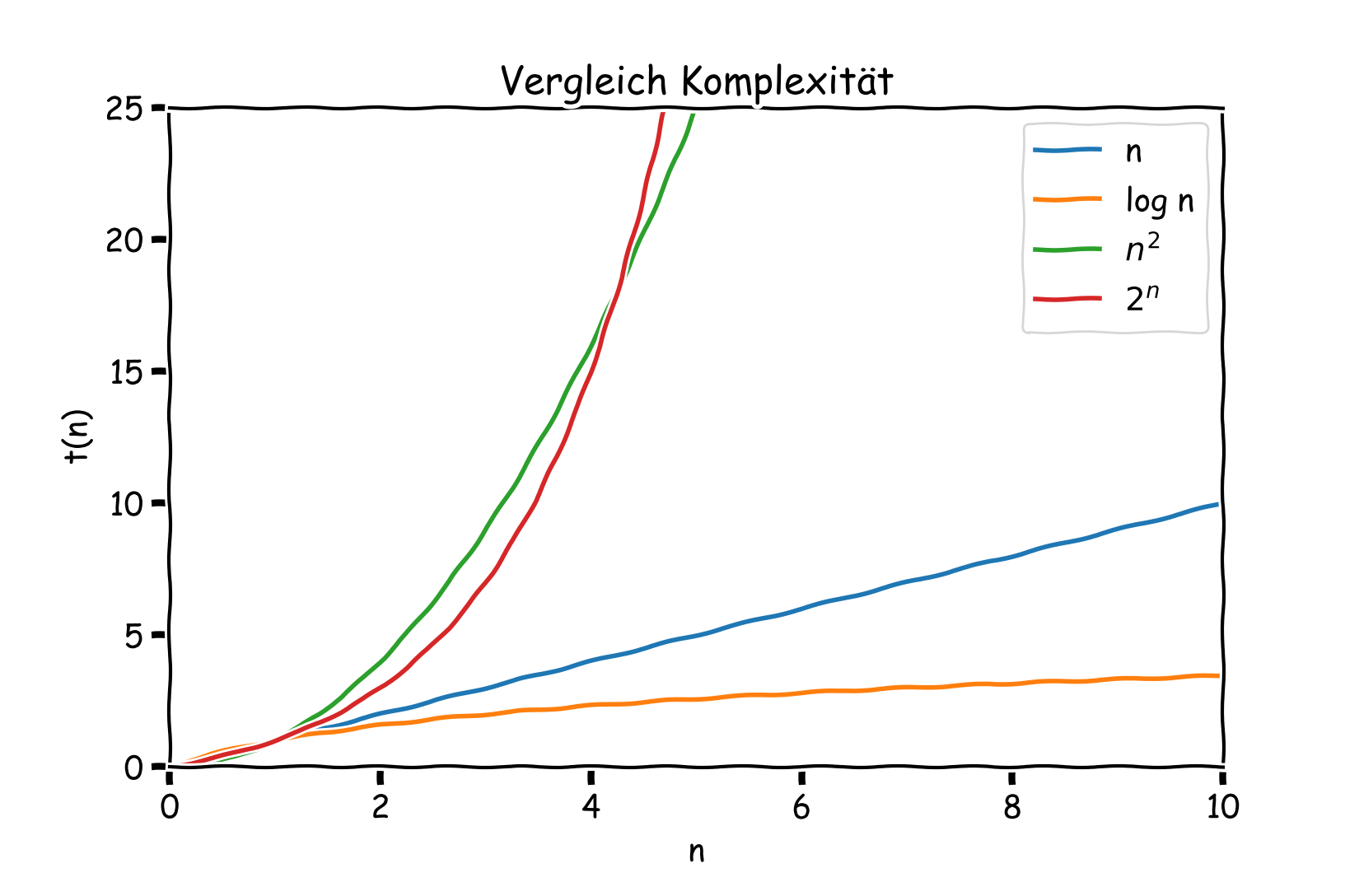
Für viele Probleme der Informatik hat man noch keine effiziente Algorithmen gefunden, also solche mit polynomialer Laufzeit oder besser.

Ein solches Beispiel ist die Faktorisierung einer Zahl in ihre Primfaktoren.

Diese Aufgabe scheint einfach, wird aber für sehr grosse Zahlen sehr aufwändig!

Es ist kein polynomiales Faktorisierungsverfahren bekannt – es kann aber auch nicht ausgeschlossen werden, dass es ein solches gibt! Dieses sogenannte P-NP-Problem ist eines der grossen ungelösten Probleme der theoretischen Informatik.