Wie könnte man die Addition zweier einstelliger Zahlen im Binären System als Schaltung konstruieren?
Die Tabelle müsste so aussehen
| Eingang A | Eingang B | Ausgang |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 10 |
Da der Ausgang nicht zweistellig sein kann, müssten wir eine Schaltung mit zwei Ausgängen konstruieren. Der erste Ausgang würde die hinterste Ziffer des Resultates der Addition beschreiben und wäre identisch mit dem exklusiven ODER. Der zweite würde den Übertrag markieren und ergäbe nur im Fall wo A und B beide 1 sind 1, was wiederum der bekannten Schaltung für UND entspricht.
Hinweis
Wichtiges Prinzip der Informatik: Ein komplexes Problem wird in kleinere, weniger komplexere Probleme unterteilt, die dann einfach gelöst werden können.
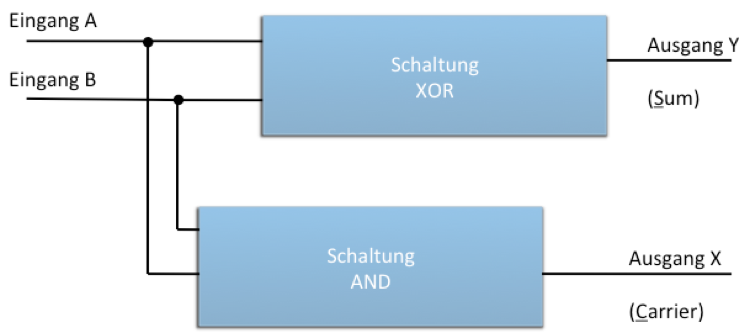
Mit dieser Schaltung erreichen wir die folgenden Wahrheitstabelle:
| Eingang A | Eingang B | Ausgang X | Ausgang Y |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Diese weit verbreitete Schaltung bezeichnet man als Halbaddierer (HA).
Aufgabe
Nimm den Logikbaukasten und verbinde die AND- und die XOR-Schaltung aus der letzten Aufgabe so, dass du einen Halbaddierer erhältst. Du brauchst nun zwei Leuchtdioden um das Ergebnis anzuzeigen.
Aufgabe
- Baue die obenstehende Schaltung mit dem Programm Logisim nach. Benutze als Eingabe zwei Knöpfe. Für die Ausgabe kannst du zwei LED-Lämpchen einfügen.
- Speichere die Schaltung als
Halbaddierer.circ: So kann sie später als Baustein in neuen Schaltungen verwendet werden. (Dazu neues File erzeugen und alte Schaltung überProjekt@fa-hand-o-right@Bibliothek laden@fa-hand-o-right@Logisim Bibliothekladen)