Mit Hilfe der While-Schleife, können wir Code wiederholt ausführen. Vor jedem Ausführen der Schleife wird eine Bedingung überprüft. Ergibt diese True, dann wird der Schleifeninhalt ausgeführt. Ergibt sie False, dann wird die Schleife beendet und der nachfolgende Code ausgeführt. Der Schleifeninhalt wird durch Einrücken gekennzeichnet.

Hinweis: Analogon

Wiederholtes Ausführen eines Schrittes, nur wenn das Ergebnis noch nicht zufriedenstellend ist: z.B. «ist der Rubiks-Cube noch nicht gelöst?» Dann weiterdrehen.

Syntax

while bedingung:
	#mach etwas

bedingung ist ein Ausdruck oder der Aufruf eines Unterprogramms der True oder False ergibt.

solange die Bedingung gilt wiederhole…

Beispiele

Feste Anzahl Wiederholungen

Möchte man etwas eine bestimmte Anzahl Mal ausführen, so kann man das einfach mit einer while-Schleife:

1. Vor der Schleife definieren wir eine Zählvariable und setzen diese auf einen sinnvollen Startwert
2. In der Bedingung überprüfen wir, wie gross der Wert unserer «Zählvariable» ist – wenn er zu gross ist, wird die Schleife abgebrochen
3. im Inhalt der Schleife erhöhen wir die «Zählvariable». (Sehr wichtig! Sonst erhalten wir eine Endlosschleife)

i = 0
while i < 10:
	print("hallo", i)
	i = i + 1
print("tschüss", i)

Zufälliger Abbruch der Schleife

Wir simulieren Würfelwürfe mit Hilfe von Zufallszahlen. Wir wollen zählen, wie viele Würfe wir brauchen, bis wir eine 6 werfen. Bei einer 6 wird die Schleife abgebrochen und die Anzahl benötigter Würfe ausgegeben:

import random

count = 0
wurf = 0

while wurf < 6:
	wurf = random.randint(1,6)
	count = count + 1
	print(str(count) + ". Wurf:", wurf)

print("Anzahl Würfe bis 6:", count)

Durch den import von random steht uns die Funktion randint() zur Verfügung. Mit random.randint(1,6) erhalten wir eine ganze Zahl zufällig zwischen 1 und 6 (inklusive 1 und 6).

Im Vergleich könnten wir auch wurf != 6 schreiben. Hier würde es klappen, da wurf vom Typ int ist. Wenn wir aber float auf Gleichheit oder Ungleichheit vergleichen, dann ist das sehr gefährlich, da kleinste Ungenauigkeiten bei Kommazahlen nicht vermeidbar sind und das zu Problemen führt. Also besser immer mit <, > oder <=, >= prüfen!

Aufgaben

Aufgabe

Simuliere Würfe mit mehreren Würfeln. Beim Yatzy hat man z.B. 6 Würfel.
Wie gross ist die Wahrscheinlichkeit, dass man im ersten Versuch alle 6 gleich hat?

Zusatzaufgabe: «𝛑 mit Monte-Carlo»

Versuche eine möglichst genaue Näherung für 𝛑 mit der unten beschriebenen Monte-Carlo-Methode zu bestimmen.
Als Erweiterung kannst du den Versuch auch grafisch darstellen.

Tipp: 𝛑 mit Monte-Carlo

Die Formel zur Berechnung der Fläche eines Kreises, beinhaltet 𝛑. Wir verteilen Punkte zufällig auf eine Fläche, die zum Teil von einem Kreis bedeckt ist. Nun stehen die Anzahl «Treffer» auf den Kreis im Verhältnis zu der Fläche des Kreises. So können wir 𝛑 statistisch bestimmen.

Zur Einfachheit schauen wir einen Viertelkreis mit Radius 1 an und verteilen die Punkte zufällig im umgebenden Quadrat:

PI statistisch^[1]

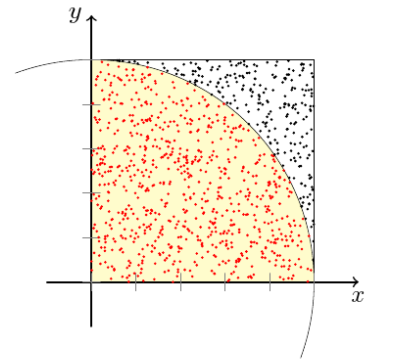
Fläche des Quadrates:

$$A_Q=r^2=1$$

Fläche des Viertelkreises:

$$A_K=\frac{r^2\cdot \pi }{4}=\frac{\pi }{4}$$

Die Wahrscheinlichkeiten, dass ein zufällig gewählter Punkt innerhalb des Viertelkreises liegt ($\text{Treffer}$), verglichen zu innerhalb des Quadrates ($\text{Versuche}$), verhalten sich gleich, wie die Flächen:

$$\frac{\text{Treffer}}{\text{Versuche}}=\frac{A_K}{A_Q}=\frac{r^2\cdot \pi /4}{r^2}=\frac{\pi }{4}$$

Wenn wir dann noch nach $\pi$ auflösen, ergibt dies:

$$\pi =4\cdot \frac{\text{Treffer}}{\text{Versuche}}$$

---

1. Springob via Wikimedia ↩︎