Steckbrief Selection Sort
- Zeitkomplexität
- Platzkomplexität
- stabil
- nein (stabile Version möglich)
- in-place
- ja
- rekursiv
- nein
Ein weiterer bekannter Sortieralgorithmus ist der Selection Sort.
Dieses Verfahren ist eigentlich relativ einfach. Von links beginnend wird jedes Element in der Liste ausgewählt und mit dem Rest der Liste auf der rechten Seite verglichen. Dann wird das ausgewählte Element mit dem kleinsten Wert in der Liste rechts davon vertauscht, sofern dieses kleiner als der aktuelle Wert sein sollte.
Dieses Verfahren nennt sich Selection Sort, weil immer das kleinste Element in einer Teilliste gesucht und ausgewählt (selected) wird. Alternativ könnte man auch von rechts startend immer das grösste Element in der Liste suchen. Alternative Namen für dieses Verfahren sind Min Sort und Max Sort.
Selection Sort verwendet drei Indizes: i repräsentiert dabei jeweils das gewählte Element, j wird gebraucht, um den Wert bei i mit jedem anderen (j) rechts davon zu vergleichen und m wird gebraucht um immer das kleinste gefundene Element zu markieren.
Das Verfahren besteht also aus 2 ineinander verschachtelten For-Schleifen:
- In der äusseren Schleife wird
i(beginnend beim ersten Element der Liste) durch die gesamte Liste iteriert. - In der inneren Schleife, beginnend bei
iwird der Wert vonimit jedem vonjverglichen. Dabei iteriertjbis zum Ende der Liste. Wird ein Wert gefunden, der kleiner als der bei i und bei ist, wird dieser mitmmarkiert.
Sobald j am Ende der Liste angekommen ist zeigt m also zum kleinsten Element zwischen i und j. Dann werden die Elemente bei i und m vertauscht, i wird um eins erhöht und das Ganze wiederholt sich.
Sobald i beim letzten Wert angekommen ist, stoppt das Verfahren.
Beispiel
Das folgende Beispiel illustriert das Verfahren anhand einer unsortierten Liste mit 5 Integer Werten.
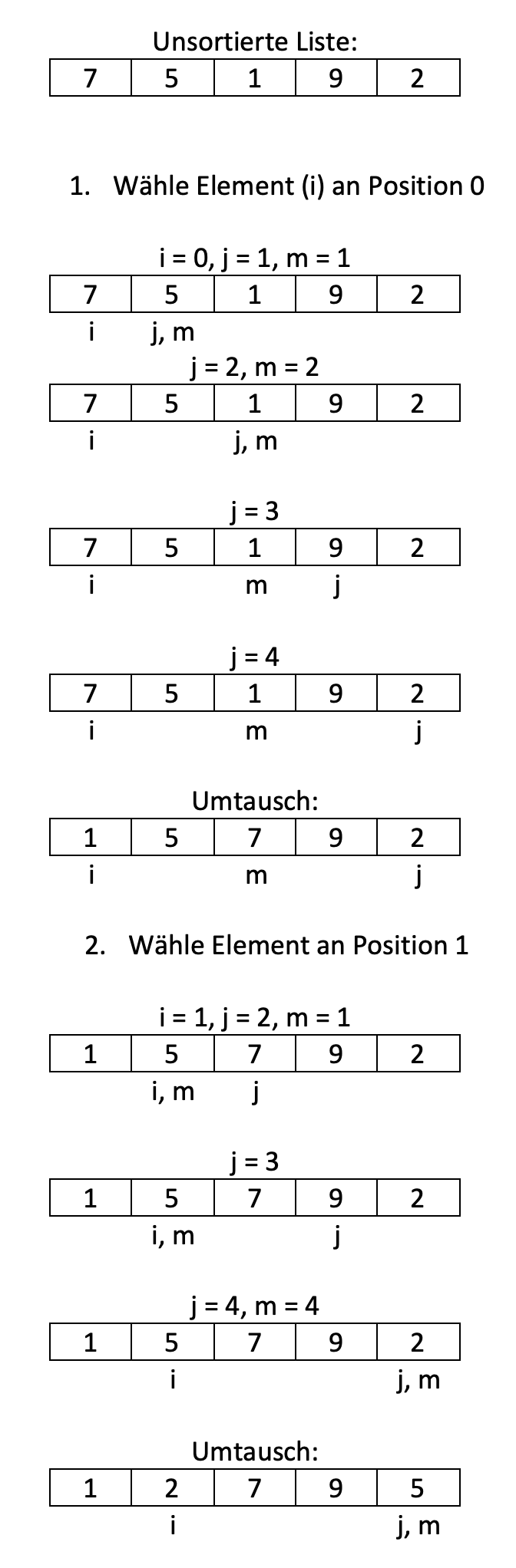
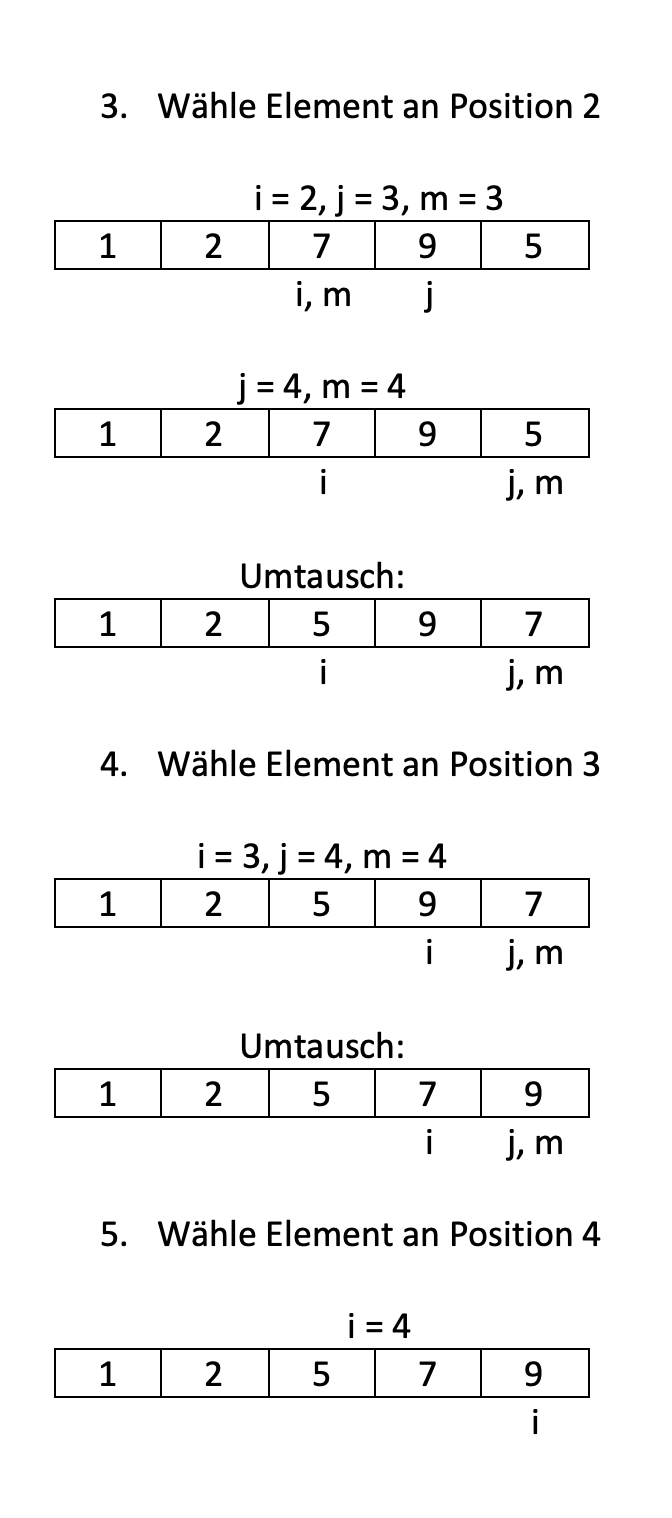
Aufgaben
Aufgabe: Papier
Wende den Sortier-Algorithmus Selection Sort auf Papier auf die Liste [7,4,2,9,1] an. Schreibe dabei alle Zwischenschritte und jeweils die Werte für i, j und m auf (siehe obiges Beispiel)!
Aufgabe: Programmieren
Kopiere das untenstehende Code-Gerüst als selection_sort.py in deine Programmierumgebung. Implementiere die Funktion selection_sort(liste).
def selection_sort(liste):
pass
liste1 = [7,3,6,13,14,9,8,12,2,11,15,1]
bubble_sort(liste1)
2
3
4
5
Tipp: Aufgabe Programmieren
Der Algorithmus lässt sich mit einer verschachtelten For-Schleife implementieren. In der äusseren For-Schleife wird jedes Element in der Liste ausgewählt. In der inneren For-Schleife wird aus der restlichen Liste (d.h. alle sich rechts vom gewählten Element befindlichen Werte) der kleinste Wert gesucht. Falls der kleinste Wert kleiner sein sollte als das gewählte Element, werden die Werte vertauscht und das nächste Element wird ausgewählt.
Aufgabe: Grafische Darstellung
Ergänze deine Funktion so, dass der Ablauf der Funktion grafisch illustriert wird (so ähnlich wie bei den bisher gesehenen Sortieralgorithmen)!
Aufgabe: Testen
Führe selection_sort mit verschiedenen Listen aus und beobachte, wie sich der Algorithmus verhält.
Versuche mit dem Programm unter anderem die folgenden Listen zu sortieren:
liste = [1,5,2,7,9,4,2,1]
liste = [2,6,9,12,15,23]
liste = [23,15,12,9,6,2]
liste = [17,2,12,8,1,9,5,12,7,3,5,4]
2
3
4