Counting sort ist ein instabiler und effizienter Sortieralgorithmus für ganze Zahlen, der auf der Idee basiert, die Häufigkeit jeder Zahl im Array zu zählen und dann die endgültige Position jeder Zahl im sortierten Array zu berechnen.

Die Schritte des Algorithmus sind:

1. Erstelle ein Array mit der Länge des grössten Wertes der Liste
2. Zähle die Häufigkeit jeder Zahl im zu untersuchenden Ausgangsarray
3. Berechne die Häufigkeiten jedes Wertes und füge diese zu dem neu erstellten Array hinzu.
4. Addiere für jeden Wert die Häufigkeiten der vorherigen Werten dazu
5. Iteriere durch das Ausgangsarray von links und platziere jede Zahl in ihre endgültige Position im sortierten Array. Nutze dabei die Zahl im neuen Array. Die Zahl im neuen Array zeigt sozusagen die Position des Wertes in der Liste. Damit Listen mit mehreren gleichen Werten sortiert werden können, muss -1 gerechnet werden.

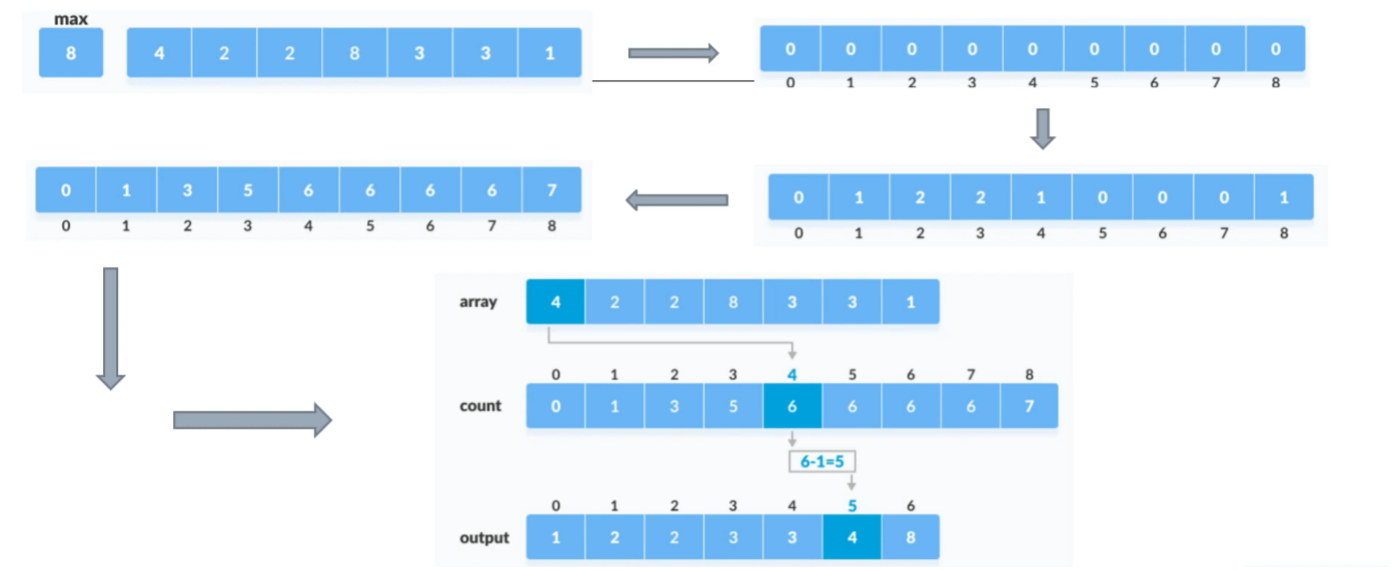
Counting Sort ist sehr effizient, da es die zu sortierenden Elemente nicht vergleicht, sondern lediglich ihre Häufigkeiten zählt. Es eignet sich daher besonders für grosse Arrays mit begrenztem Wertbereich. Allerdings ist der Algorithmus nicht stabil.

RANGE = 10

def countingSort(liste):
	size = len(liste)
	output = [0] * size
	count = [0] * RANGE

	# zähle Werte
	for zahl in liste:
		count[zahl] += 1
		
	print("      Zählliste:", count)

	# addiere gezählte Werte
	for i in range(1, RANGE):
		count[i] += count[i - 1]

	print(" Additionsliste:", count)
	
	# setze Werte an korrekte Position
	for zahl in liste:
		output[count[zahl]-1] = zahl
		count[zahl] -= 1

	# kopiere neue Liste über Original-Liste
	for i in range(0, size):
		liste[i] = output[i]


liste = [4, 2, 2, 8, 3, 3, 1, 2, 3]
print("          Liste:", liste)
countingSort(liste)
print("Sortierte Liste:", liste)