Im Folgenden versuchen wir, die in den letzten Kapiteln kennengelernten Grundprinzipien der Objektorientierten Programmierung zusammenzufassen:
Abstraktion
Definition: Abstraktion
Abstraktion bedeutet, die wesentlichen, bedeutsamsten Eigenschaften von etwas zu identifizieren, während man gleichzeitig alles Nebensächliche und Unbedeutende verwirft.
In der OOP kommt die Abstraktion im Design-Prozess vor: Dabei müssen Klassen als Vorlage für Objekte und ihre Eigenschaften definiert werden. Wir müssen uns überlegen, welche Elemente zentral sind und wie wir diese festhalten können. Nebensächliche Dinge können vergessen werden.
mehr: Analogie zur Abstraktion
In der Gestaltung wird häufig abstrahiert – so z.B. beim Erstellen einer Illustration. Dabei kann verschieden weit gegangen werden:
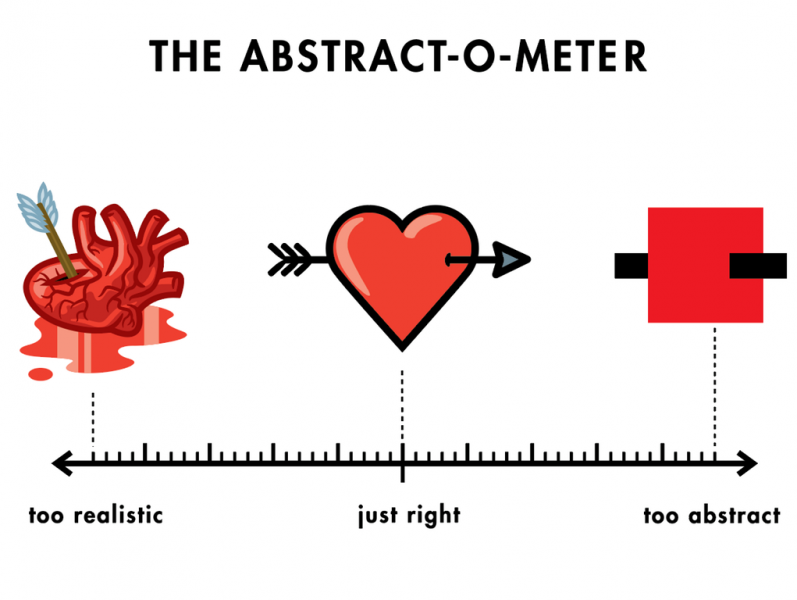
Aufgabe: Geometrie
Du hast den Auftrag, eine Geometrie-Programm zu schreiben:
- Im Programm sollen geometrische Formen so definiert werden, dass Ihr Umfang und ihre Fläche berechnet werden kann
- Folgende Formen sollen als Klasse dargestellt werden:
Kreis,QuadratundDreieck - Die Formen sollen in der Ebene gezeichnet werden können. Zur Unterscheidung kann den Formen eine Farbe zugewiesen werden
Überlege dir, welche Eigenschaften welche Klasse haben muss. Halte deine Überlegungen in einem Klassen-Diagramm fest.
Lösung: Diagramm
Zusatzaufgabe: Geometrie
Beginne mit einer Umsetzung der Klassen in Python
Lösung: Python-Code
from dreieck import Dreieck
from kreis import Kreis
from quadrat import Quadrat
q = Quadrat("red", 2)
print(q.flaeche())
k = Kreis("green", 5)
print(k.umfang())
d = Dreieck("blue", 4, 7, 34)
print(d.flaeche())from math import pi
class Kreis:
def __init__(self, farbe, radius):
self.farbe = farbe
self.radius = radius
def umfang(self):
return 2 * self.radius * pi
def flaeche(self):
return self.radius**2 * piclass Quadrat:
def __init__(self, farbe, seite):
self.farbe = farbe
self.seite = seite
def umfang(self):
return 4*self.seite
def flaeche(self):
return self.seite**2class Dreieck:
def __init__(self, farbe, seite, hoehe, winkel):
self.farbe = farbe
self.seite = seite
self.hoehe = hoehe
self.winkel = winkel
def umfang(self):
return 42
def flaeche(self):
return self.seite * self.hoeheVererbung
Definition: Vererbung
Mittels Vererbung kann eine neue Klasse aufbauend auf einer existierenden Klasse geschaffen werden. Die Beziehung zwischen neuer und bestehender Klasse ist dauerhaft.
Wir können schon OOP ohne Vererbung betreiben. Aber häufig haben wir leichte Variationen von Objekten und es lohnt sich diese mit verschieden Spezialisierungen einer gemeinsamen Oberklasse darzustellen.
So könnten sich die Klassen dog und sheep in diversen Punkten unterscheiden. Da beide aber viele Gemeinsamkeiten haben, lohnt es sich, diese in einer Oberklasse Animal zusammenzutragen:
mehr: Analogie zur Vererbung
Menschen geben Gene weiter. Von dort kommt wohl auch der Begriff «Vererbung».

Aufgabe: Geometrie
Erweitere die letzte Aufgabe, indem du eine Oberklasse Form einführst, wovon die drei Klassen Kreis, Quadrat und Dreieck erben.
Welche Eigenschaften und Methoden können nun in die neue Klasse Form verlegt und dann an die 3 Unterklassen vererbt werden? Zeichne ein neues Klassendiagramm.
Lösung: Diagramm
Zusatzaufgabe: Geometrie
Arbeite an deiner Umsetzung der Klassen in Python
Lösung: Python-Code
from dreieck import Dreieck
from kreis import Kreis
from quadrat import Quadrat
q = Quadrat("red", 2)
print(q.flaeche())
k = Kreis("green", 5)
print(k.umfang())
d = Dreieck("blue", 4, 7, 34)
print(d.flaeche())class Form:
def __init__(self, farbe):
self.farbe = farbe
def umfang(self):
return 0
def flaeche(self):
return 0from form import Form
from math import pi
class Kreis(Form):
def __init__(self, farbe, radius):
super().__init__(farbe)
self.radius = radius
def umfang(self):
return 2 * self.radius * pi
def flaeche(self):
return self.radius**2 * pifrom form import Form
class Quadrat(Form):
def __init__(self, farbe, seite):
super().__init__(farbe)
self.seite = seite
def umfang(self):
return 4*self.seite
def flaeche(self):
return self.seite**2from form import Form
class Dreieck(Form):
def __init__(self, farbe, seite, hoehe, winkel):
super().__init__(farbe)
self.seite = seite
self.hoehe = hoehe
self.winkel = winkel
def umfang(self):
return 42
def flaeche(self):
return self.seite * self.hoeheDatenkapselung
Definition: Datenkapselung
Datenkapselung (encapsulation) bezeichnet in der Informatik das bewusste Verbergen von Daten vor dem Zugriff von aussen. Der Zugriff von aussen wir durch eine Schnittstelle geregelt.
Wenn die Verwendung einer Klasse, resp. Objekte dieser Klasse nur über eine Schnittstelle (den Konstruktor, die Methoden) läuft, dann kann uns eigentlich das Innere der Klasse egal sein. Die Klasse liesse sich sogar ersetzen durch eine mit denselben Schnittstellen, aber einer völlig anderen internen Implementation.
Wir könnten das Alter einer Person statt als Alter (person_simple.py), als Jahrgang (person.py) speichern. Solange die Schnittstellen korrekt sind, funktioniert unser main.py mit beiden Varianten:
from person import Person
hagrid = Person("Hagrid", 41)
print(hagrid.getAge())class Person:
def __init__(self, name, age):
self._name = name
self._age = age
def getAge(self):
return self._agefrom datetime import date
class Person:
def __init__(self, name, age):
self._name = name
today = date.today()
self._yearOfBirth = today.year - age
def getAge(self):
today = date.today()
return today.year - self._yearOfBirthmehr: Analogie zur Datenkapselung
In der Medizin gibt es Pillen in der Form von Kapseln. Diese können unterschiedliche Wirkstoffe beinhalten, ohne dass wir diese sehen. Wir können diese Wirkstoffe alle aufs Mal einnehmen und die Pille könnte ersetzt werden mit ganz anderen Elementen, solange die Wirkung gleich bleibt, würden wir uns nicht beklagen.
Aufgabe: Geometrie
Kannst du im obigen Beispiel Datenkapselung einbauen? Überlege dir wo dies Sinn macht, resp. welche Eigenschaften möchten wir wie zugreifbar machen. Ergänze das Klassen-Diagramm entsprechend.
Lösung
Zusatzaufgabe: Geometrie
Arbeite an deiner Umsetzung der Klassen in Python
Lösung: Python-Code
from dreieck import Dreieck
from kreis import Kreis
from quadrat import Quadrat
q = Quadrat("red", 2)
print(q.flaeche())
k = Kreis("green", 5)
print(k.umfang())
d = Dreieck("blue", 4, 7, 34)
print(d.flaeche())class Form:
def __init__(self, farbe):
self._farbe = farbe
def umfang(self):
return 0
def flaeche(self):
return 0from form import Form
from math import pi
class Kreis(Form):
def __init__(self, farbe, radius):
super().__init__(farbe)
self.__radius = radius
def umfang(self):
return 2 * self.__radius * pi
def flaeche(self):
return self.__radius**2 * pifrom form import Form
class Quadrat(Form):
def __init__(self, farbe, seite):
super().__init__(farbe)
self.__seite = seite
def umfang(self):
return 4*self.__seite
def flaeche(self):
return self.__seite**2from form import Form
class Dreieck(Form):
def __init__(self, farbe, seite, hoehe, winkel):
super().__init__(farbe)
self.__seite = seite
self.__hoehe = hoehe
self.__winkel = winkel
def umfang(self):
return 42
def flaeche(self):
return self.__seite * self.__hoehePolymorphie
Definition: Polymorphie
Mittels Vererbung ist es möglich, dass ein Objekt «vielgestaltig» ist: Eine Unterklasse kann Methoden der Oberklasse überschreiben. Zur Laufzeit wird dann entschieden, welche Methode ausgeführt wird.
mehr: Analogie zur Polymorphie
Wasser hat bekanntlich mehrere Zustände – zwar nicht gleichzeitig.
Aufgabe: Geometrie
Wie würde eine Funktion aussehen, die eine Liste von Geometrischen Objekten erhält und die Flächen addiert?
- Schreibe so eine Funktion mit Python.
- wie kommt dabei Polymorphie zum Einsatz?
Zusatzaufgabe: Geometrie
Stelle die Umsetzung der Klassen in Python fertig
Lösung: Python-Code
from dreieck import Dreieck
from kreis import Kreis
from quadrat import Quadrat
q = Quadrat("red", 2)
k = Kreis("green", 5)
d = Dreieck("blue", 4, 7, 34)
liste = [q, k, d]
summe = 0
for s in liste:
summe = summe + s.flaeche()
print("gesamtfläche:", summe)class Form:
def __init__(self, farbe):
self._farbe = farbe
def umfang(self):
return 0
def flaeche(self):
return 0from form import Form
from math import pi
class Kreis(Form):
def __init__(self, farbe, radius):
super().__init__(farbe)
self.__radius = radius
def umfang(self):
return 2 * self.__radius * pi
def flaeche(self):
return self.__radius**2 * pifrom form import Form
class Quadrat(Form):
def __init__(self, farbe, seite):
super().__init__(farbe)
self.__seite = seite
def umfang(self):
return 4*self.__seite
def flaeche(self):
return self.__seite**2from form import Form
class Dreieck(Form):
def __init__(self, farbe, seite, hoehe, winkel):
super().__init__(farbe)
self.__seite = seite
self.__hoehe = hoehe
self.__winkel = winkel
def umfang(self):
return 42
def flaeche(self):
return self.__seite * self.__hoeheZusammenfassung
Ein kurzes Video das auf die 4 Grundprinzipien eingeht und jeweils Beispiele bringt: