Als Beispiel für unsupervised learning schauen wir uns den ML-Algorithmus k-means an. Der Algorithmus unterteilt Merkmalsvektoren in k Klassen (sogenannte Cluster).
Algorithmus
- Wähle zufällig k Punkte, sogenannte Clusterzentren (clustroids)
- Ordne jeden Punkt dem nächsten Clusterzentrum zu
- Berechne neue Clusterzentren als Gravitationsmittelpunkt jedes Clusters
- Wiederhole Schritte 2 und 3
Beispiel
Wir schauen uns den Algorithmus an folgendem Beispiel an und beziehen uns dabei auf die oben genannten 4 Schritte:
Ausgangslage
Die grau eingetragenen Punkte sollen in 3 Cluster unterteilt werden.
Schritt 1
Es werden zufällig drei Clusterzentren gewählt.
(in der Abbildung farbig hervorgehoben)
Alternativ könnte man auch 3 vorhandene Punkte als Clusterzentrum auswählen.
Schritt 2
Alle Punkte werden ihrem nächsten Clusterzentrum zugeordnet: es entstehen 3 Cluster.
(in der Abbildung farbig hervorgehoben)
Schritt 3
Für jeden Cluster wird das Gravitationszentrum berechnet. Anschliessend wird das Clusterzentrum auf das Gravitationszentrum gesetzt.
Wiederholung
Die Schritte 2 und 3 werden mehrmals wiederholt. Die Clusterzentren verschieben sich dabei immer weniger.
Am Schluss erhalten wir die gewünschten 3 Cluster.
Aufgabe: Endzustand
Überlege dir, wie die 3 Cluster am Schluss aussehen würden, wenn man die Schritte 2 und 3 noch mindestens 5 Mal wiederholt
Python
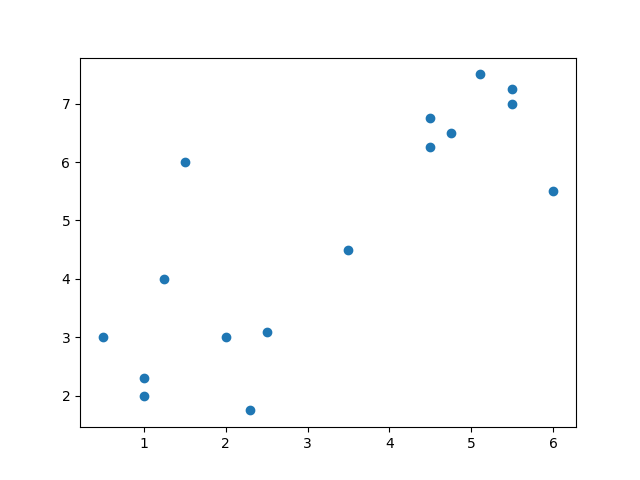
Wir verwenden wiederum die Werte von Heinz-Willhelms Pilzmaschine, entfernen aber die Labels und nehmen die beiden später gefundenen Pilze gleich dazu. Unsere Punkte sind wie folgt angeordnet und sollen in 2 Cluster unterteilt werden.
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
data = [
(1, 2),
(0.5, 3),
(1.25, 4),
(2.3, 1.75),
(1, 2.3),
(2.5, 3.1),
(1.5, 6),
(5.5, 7),
(6, 5.5),
(5.5, 7.25),
(4.5, 6.75),
(4.5, 6.25),
(4.75, 6.5),
(5.1, 7.5),
(2, 3),
(3.5, 4.5)
]
x_points = [point[0] for point in data]
y_points = [point[1] for point in data]
plt.scatter(x_points, y_points)
plt.show()
plt.close()Aufgabe: a oder b?
Gehe vom obenstehenden Beispiel aus und versuche, diese Daten in 2 Cluster zu unterteilen.
- du löst das Ganze selbst, indem du eigene Funktionen zur Clusterzentren-Berechnung und Cluster-Bildung definierst
- du verwendest
KMeansaus dem Paketsklearn.cluster
mehr: Tipp zu Teilaufgabe b
KMeans kann wie folgt aufgerufen werden:
from sklearn.cluster import KMeans
...
kmeans = KMeans(n_clusters=2, init='k-means++', max_iter=300, n_init=10, random_state=0)
y_kmeans = kmeans.fit_predict(data)bleibt noch die Interpretation des Resultats y_kmeans. Schön wäre, wenn wir die Punkte wirklich farbig darstellen können!
Iris-Dataset
Für den sogenannten Iris-Datensatz wurden von 3 verschiedenen Schwertlilien-Arten je 50 Exemplare ausgemessen. Die Messerwert sind Länge und Breite des Kelchblatt (sepal) sowie Länge und Breite des Blütenblatts (petal).
Der Datensatz liegt im CSV-Format vor:
"sepal.length","sepal.width","petal.length","petal.width","variety"
5.1,3.5,1.4,.2,"Setosa"
4.9,3,1.4,.2,"Setosa"
4.7,3.2,1.3,.2,"Setosa"
4.6,3.1,1.5,.2,"Setosa"
5,3.6,1.4,.2,"Setosa"
5.4,3.9,1.7,.4,"Setosa"
4.6,3.4,1.4,.3,"Setosa"
5,3.4,1.5,.2,"Setosa"
4.4,2.9,1.4,.2,"Setosa"
4.9,3.1,1.5,.1,"Setosa"
5.4,3.7,1.5,.2,"Setosa"
4.8,3.4,1.6,.2,"Setosa"
4.8,3,1.4,.1,"Setosa"
4.3,3,1.1,.1,"Setosa"
5.8,4,1.2,.2,"Setosa"
5.7,4.4,1.5,.4,"Setosa"
5.4,3.9,1.3,.4,"Setosa"
5.1,3.5,1.4,.3,"Setosa"
5.7,3.8,1.7,.3,"Setosa"
5.1,3.8,1.5,.3,"Setosa"
5.4,3.4,1.7,.2,"Setosa"
5.1,3.7,1.5,.4,"Setosa"
4.6,3.6,1,.2,"Setosa"
5.1,3.3,1.7,.5,"Setosa"
4.8,3.4,1.9,.2,"Setosa"
5,3,1.6,.2,"Setosa"
5,3.4,1.6,.4,"Setosa"
5.2,3.5,1.5,.2,"Setosa"
5.2,3.4,1.4,.2,"Setosa"
4.7,3.2,1.6,.2,"Setosa"
4.8,3.1,1.6,.2,"Setosa"
5.4,3.4,1.5,.4,"Setosa"
5.2,4.1,1.5,.1,"Setosa"
5.5,4.2,1.4,.2,"Setosa"
4.9,3.1,1.5,.2,"Setosa"
5,3.2,1.2,.2,"Setosa"
5.5,3.5,1.3,.2,"Setosa"
4.9,3.6,1.4,.1,"Setosa"
4.4,3,1.3,.2,"Setosa"
5.1,3.4,1.5,.2,"Setosa"
5,3.5,1.3,.3,"Setosa"
4.5,2.3,1.3,.3,"Setosa"
4.4,3.2,1.3,.2,"Setosa"
5,3.5,1.6,.6,"Setosa"
5.1,3.8,1.9,.4,"Setosa"
4.8,3,1.4,.3,"Setosa"
5.1,3.8,1.6,.2,"Setosa"
4.6,3.2,1.4,.2,"Setosa"
5.3,3.7,1.5,.2,"Setosa"
5,3.3,1.4,.2,"Setosa"
7,3.2,4.7,1.4,"Versicolor"
6.4,3.2,4.5,1.5,"Versicolor"
6.9,3.1,4.9,1.5,"Versicolor"
5.5,2.3,4,1.3,"Versicolor"
6.5,2.8,4.6,1.5,"Versicolor"
5.7,2.8,4.5,1.3,"Versicolor"
6.3,3.3,4.7,1.6,"Versicolor"
4.9,2.4,3.3,1,"Versicolor"
6.6,2.9,4.6,1.3,"Versicolor"
5.2,2.7,3.9,1.4,"Versicolor"
5,2,3.5,1,"Versicolor"
5.9,3,4.2,1.5,"Versicolor"
6,2.2,4,1,"Versicolor"
6.1,2.9,4.7,1.4,"Versicolor"
5.6,2.9,3.6,1.3,"Versicolor"
6.7,3.1,4.4,1.4,"Versicolor"
5.6,3,4.5,1.5,"Versicolor"
5.8,2.7,4.1,1,"Versicolor"
6.2,2.2,4.5,1.5,"Versicolor"
5.6,2.5,3.9,1.1,"Versicolor"
5.9,3.2,4.8,1.8,"Versicolor"
6.1,2.8,4,1.3,"Versicolor"
6.3,2.5,4.9,1.5,"Versicolor"
6.1,2.8,4.7,1.2,"Versicolor"
6.4,2.9,4.3,1.3,"Versicolor"
6.6,3,4.4,1.4,"Versicolor"
6.8,2.8,4.8,1.4,"Versicolor"
6.7,3,5,1.7,"Versicolor"
6,2.9,4.5,1.5,"Versicolor"
5.7,2.6,3.5,1,"Versicolor"
5.5,2.4,3.8,1.1,"Versicolor"
5.5,2.4,3.7,1,"Versicolor"
5.8,2.7,3.9,1.2,"Versicolor"
6,2.7,5.1,1.6,"Versicolor"
5.4,3,4.5,1.5,"Versicolor"
6,3.4,4.5,1.6,"Versicolor"
6.7,3.1,4.7,1.5,"Versicolor"
6.3,2.3,4.4,1.3,"Versicolor"
5.6,3,4.1,1.3,"Versicolor"
5.5,2.5,4,1.3,"Versicolor"
5.5,2.6,4.4,1.2,"Versicolor"
6.1,3,4.6,1.4,"Versicolor"
5.8,2.6,4,1.2,"Versicolor"
5,2.3,3.3,1,"Versicolor"
5.6,2.7,4.2,1.3,"Versicolor"
5.7,3,4.2,1.2,"Versicolor"
5.7,2.9,4.2,1.3,"Versicolor"
6.2,2.9,4.3,1.3,"Versicolor"
5.1,2.5,3,1.1,"Versicolor"
5.7,2.8,4.1,1.3,"Versicolor"
6.3,3.3,6,2.5,"Virginica"
5.8,2.7,5.1,1.9,"Virginica"
7.1,3,5.9,2.1,"Virginica"
6.3,2.9,5.6,1.8,"Virginica"
6.5,3,5.8,2.2,"Virginica"
7.6,3,6.6,2.1,"Virginica"
4.9,2.5,4.5,1.7,"Virginica"
7.3,2.9,6.3,1.8,"Virginica"
6.7,2.5,5.8,1.8,"Virginica"
7.2,3.6,6.1,2.5,"Virginica"
6.5,3.2,5.1,2,"Virginica"
6.4,2.7,5.3,1.9,"Virginica"
6.8,3,5.5,2.1,"Virginica"
5.7,2.5,5,2,"Virginica"
5.8,2.8,5.1,2.4,"Virginica"
6.4,3.2,5.3,2.3,"Virginica"
6.5,3,5.5,1.8,"Virginica"
7.7,3.8,6.7,2.2,"Virginica"
7.7,2.6,6.9,2.3,"Virginica"
6,2.2,5,1.5,"Virginica"
6.9,3.2,5.7,2.3,"Virginica"
5.6,2.8,4.9,2,"Virginica"
7.7,2.8,6.7,2,"Virginica"
6.3,2.7,4.9,1.8,"Virginica"
6.7,3.3,5.7,2.1,"Virginica"
7.2,3.2,6,1.8,"Virginica"
6.2,2.8,4.8,1.8,"Virginica"
6.1,3,4.9,1.8,"Virginica"
6.4,2.8,5.6,2.1,"Virginica"
7.2,3,5.8,1.6,"Virginica"
7.4,2.8,6.1,1.9,"Virginica"
7.9,3.8,6.4,2,"Virginica"
6.4,2.8,5.6,2.2,"Virginica"
6.3,2.8,5.1,1.5,"Virginica"
6.1,2.6,5.6,1.4,"Virginica"
7.7,3,6.1,2.3,"Virginica"
6.3,3.4,5.6,2.4,"Virginica"
6.4,3.1,5.5,1.8,"Virginica"
6,3,4.8,1.8,"Virginica"
6.9,3.1,5.4,2.1,"Virginica"
6.7,3.1,5.6,2.4,"Virginica"
6.9,3.1,5.1,2.3,"Virginica"
5.8,2.7,5.1,1.9,"Virginica"
6.8,3.2,5.9,2.3,"Virginica"
6.7,3.3,5.7,2.5,"Virginica"
6.7,3,5.2,2.3,"Virginica"
6.3,2.5,5,1.9,"Virginica"
6.5,3,5.2,2,"Virginica"
6.2,3.4,5.4,2.3,"Virginica"
5.9,3,5.1,1.8,"Virginica"Das CSV-Format (comma-separated-values) enthält durch Komma-getrennte Datensätze (zeilenweise). Die ersten 4 Einträge sähen in Tabellenform wie folgt aus:
| sepal.length | sepal.width | petal.length | petal.width | variety |
|---|---|---|---|---|
| 5.1 | 3.5 | 1.4 | .2 | Setosa |
| 4.9 | 3 | 1.4 | .2 | Setosa |
| 4.7 | 3.2 | 1.3 | .2 | Setosa |
| 4.6 | 3.1 | 1.5 | .2 | Setosa |
Die Datei lässt sich hier runterladen:
Die Python-Library pandas eignet sich, um Daten aus externen Dateien zu lesen. Das folgende Skript liest die Datei iris.csv (muss im selben Verzeichnis liegen wie das Skript) und extrahiert daraus die Spalten mit den Merkmalen sowie diejenige mit den Labels.
import pandas as pd
iris = pd.read_csv('iris.csv')
X = iris[["sepal.length", "sepal.width", "petal.length", "petal.width"]].values
y = iris["variety"].valuesAufgabe
Schaffst du es, das Iris-Datenset in 3 Cluster zu unterteilen?
Tiia Monto via Wikimedia Commons, CC BY-SA 4.0 ↩︎
unknown via Wikimedia Commons, CC BY-SA 3.0 ↩︎
Frank Mayfield via Wikimedia Commons, CC BY-SA 2.0 ↩︎


