Wir erforschen die Komplexität am Beispiel der Suche: Gegeben sei eine Liste mit Namen.

liste = ["Finn", "Gian", "Philipp", "Samantha", "Vincent", "Pascal", "Geremia", "Janis", "Kenneth", "Max", "Roman"]

Wir suchen nun einen gegebenen Namen in der Liste – d.h. wir möchten wissen ob und wo dieser Name in der Liste vorkommt.

Es gibt nun «intelligente» und «weniger intelligente» Möglichkeiten, diese Liste nach einem bestimmten Element zu durchsuchen.

Lineare Suche

Wir gehen die Liste Element um Element durch und vergleichen die Elemente mit dem gesuchten Element:

Suche noch nicht gestartet. Gib einen Suchbegriff ein und starte die Suche.

---

FinnGianPhilippSamanthaVincentPascalGeremiaJanisKennethMaxRoman

0 Schritte

liste = ["Finn", "Gian", "Philipp", "Samantha", "Vincent", "Pascal", "Geremia", "Janis", "Kenneth", "Max", "Roman"]

def suche_linear(liste, begriff):
	i = 0
	for eintrag in liste:
		i = i + 1
		if eintrag == begriff:
			return i

Wir zählen wie viele Elemente wir vergleichen müssen und geben diese Zahl aus.

best case

Der beste Fall wäre die Suche nach «Finn» – hier können wir gleich beim ersten Element die Suche abbrechen.

worst case

Der schlechteste Fall wäre die Suche nach «Roman» – hier müssen wir alle Elemente durchgehen und werden erst beim letzten fündig. (oder gleich schlecht: die Suche nach einem Namen der gar nicht vorkommt!)

average case

Im Durchschnitt werden wir in der Hälfte der Liste fündig!

Uns interessiert aber der schlechteste Fall! – Wenn ein Programm im Schnitt einige Sekunden benötigt, aber dann im schlechtesten Fall trotzdem ein Jahr, ist es nicht wirklich brauchbar!

Komplexität

Was ist nun, wenn wir die Liste verlängern? Dann steigt die Anzahl der Vergleiche natürlich auch: Für eine doppelt so lange Liste müssen wir auch doppelt so viele Vergleiche anstellen.

Wir haben hier also ein lineares Wachstum, welches wir in der sogenannten O-Notation wie folgt schreiben:

---

Die lineare Suche gehört zu den Funktionen der Klasse
$\mathcal{O}(n)$

---

Binäre Suche

Eine «intelligentere Suche» setzt voraus, dass die Liste sortiert ist. Wir sortieren also unsere Liste und erhalten:

liste = ["Finn", "Geremia", "Gian", "Janis", "Kenneth", "Max", "Pascal", "Philipp", "Roman", "Samantha", "Vincent"]

Wir vergleichen nun unser gesuchtes Element mit dem Element in der Mitte der Liste. Kommt unser gesuchtes Element im Alphabet nach dem Element in der Mitte, so halbieren wir die Liste und gucken uns nun nur noch den zweiten Teil an. Dort wiederholen wir das Prozedere, bis wir das Element finden.

Suche noch nicht gestartet. Gib einen Suchbegriff ein oder klicke auf einen Namen und starte die Suche.

---

FinnGeremiaGianJanisKennethMaxPascalPhilippRomanSamanthaVincent

0 Schritte

Durch das Halbieren entsteht ein binärer Baum:

«Binäre Suche»

«Max» ist genau in der Mitte, «Gian» und «Roman» sind in der Mitte der beiden Hälften, usw. Mit jedem Vergleich halbieren wir also die Menge der in Frage kommenden Elemente.

Wir kommen in diesem Beispiel in maximal 4 Schritten zu unserem Ziel.
(Der Baum hat 4 Ebenen)

Komplexität

Da die Liste nach jedem Aufruf halbiert wird, haben wir nach dem ersten Teilen noch $n/2$ Elemente, nach dem zweiten Schritt $n/4$ Elemente, nach dem dritten Schritt $n/8$ Elemente, usw. Daher lässt sich allgemein sagen, dass im i-ten Schritt maximal $n/2^i$ Elemente übrigbleiben. Das ergibt $lo{g}_{2}n$ Vergleiche bei der Suche.

Diese Suche hat also kein lineares Verhalten mehr, sondern ein logarithmisches. Wir notieren das in der O-Notation wie folgt:

---

Die binäre Suche gehört zu den Funktionen der Klasse
$\mathcal{O}(\log n)$

---

Die binäre Suche ist also schneller als die lineare. Gerade bei längeren Listen macht sich das sehr stark bemerkbar:

Komplexität unterschiedlich langer Listen

Such-	Anzahl Elemente der Liste
Algorithmus	10	50	n
linear	10	50	$n$
binär	4	6	$\log n$

Die Liste muss vorher sortiert werden! – eine Liste zu sortieren lohnt sich für eine einzige Suche aber nicht!

Code

Eine Möglichkeit, die binäre Suche zu implementieren, sieht wie folgt aus:

liste = ["Finn", "Geremia", "Gian", "Janis", "Kenneth", "Max", "Pascal", "Philipp", "Roman", "Samantha", "Vincent"]

def suche_binaer(liste, begriff):
	i = 0
	min = 0
	max = len(liste)	
	while True:
		index = (max + min) // 2
		eintrag = liste[index]
		i = i + 1		
		if eintrag == begriff:
			return i
		elif eintrag < begriff:
			min = index
		else:
			max = index

Es wird immer nur ein Teil der Liste durchsucht, der nach jedem Schritt kleiner wird. Der Teil der Liste wird durch die Variablen min und max eingegrenzt.

Zusatzaufgabe

Die Binäre Suche lässt sich sehr schön rekursiv programmieren. Dabei ruft sich die Funktion selbst auf, aber nur mit der Listenhälfte, worin sich das gesuchte Element befinden muss.

experimenteller Vergleich

Aufgabe: JupyterLab

JupyterLab ist eine Python-Umgebung welche im Browser ausgeführt wird. Das Spezielle: ein Programm kann im Blöcke unterteilt werden und schrittweise ausgeführt werden. Dazwischen können Notiz- und Ausgabe-Blöcke das ganze erweitern – es entsteht ein interaktives Skript.

Unter dem folgenden Link kannst du JupyterLab starten:

jupyter.org/try-jupyter/lab/

Untenstehend findest du eine integrierte JupyterLab-Datei mit der Endung ipynb. Diese wird hier im Skript angezeigt. Du kannst sie aber auch herunterladen und dann als JupyterLab-Datei öffnen, ausführen und bearbeiten!

1. Lade die Datei runter (klick auf Dateinamen rechts oben oder mit Button ganz am Ende)
2. Öffne den obenstehenden JupyterLabs-Link
3. Lade die heruntergeladene Datei ins JupyterLabs rauf
4. Arbeite dich durch das Notebook hindurch
   • Lies die Notizen
   • führe Code-Teile aus
   • Schau dir den entstehenden Output an
5. Versuche die experimentell ermittelten Werte mittels Excel darzustellen
6. Zusatzaufgaben
   • Verlängere die Liste, um einen schöneren Graphen zu erhalten
   • Programmiere und Teste eine rekursive Funktion für die Binäre Suche

mehr: JupyterLab installieren

JupyterLab ist eine Webanwendung. Eine lokale Installation ist aber dank dem verlinkten WebApp-Bundle relativ einfach:

github.com/jupyterlab/jupyterlab-desktop

JupyterLabsuche.ipynb

suche.ipynb

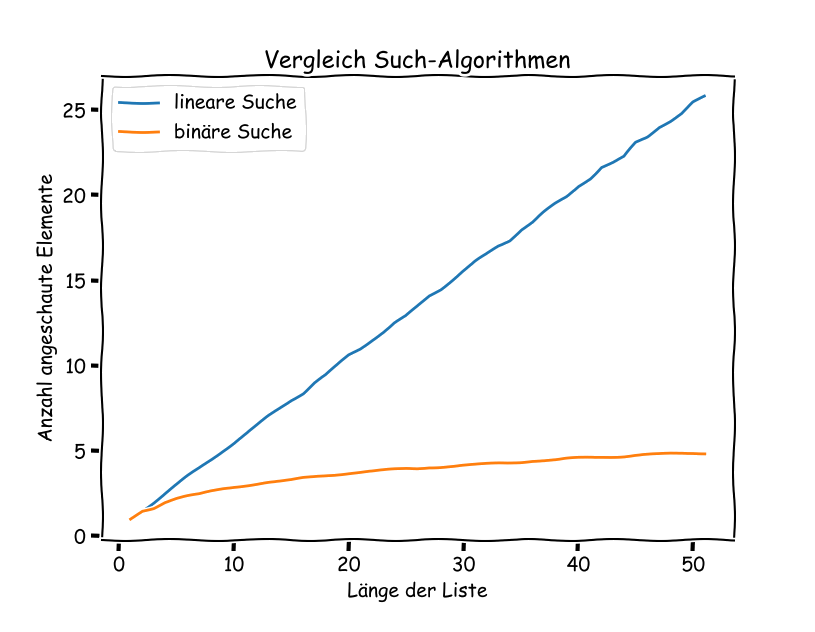
Wir können die Liste etwas vergrössern, um eine schönere Darstellung zu erhalten. Für eine Liste der Länge 50 führt dies zu folgendem Output:

«Messung Experiment»