Quick Sort

Hinweis: Steckbrief Quick Sort

Zeitkomplexität: $O (n \log n)$
Platzkomplexität: $O (n)$
stabil: nein
in-place: nein
rekursiv: ja

Bei Quick Sort wird die Liste immer wieder unterteilt: Dabei wird von der Bestehenden Liste ein sogenanntes Pivot-Element festgelegt. Alles was kleiner als dieses Element ist, kommt in die linke Liste, alles was grösser als das Pivot-Element ist, kommt in die rechte Liste.

Dieser Vorgang wird nun für die beiden neuen Listen rekursiv wiederholt.

Im Beispiel wird als Pivot-Element immer das letzte Element der Liste gewählt:

unsortierte Liste

Pivot 8 wählen

2 Listen generieren

2	7	1	6		8		15	9	20	12
	<8							>=8

Pivot 6 und Pivot 12

je Pivot 2 Listen generieren

2	1		6		7			9		12		15	20
<6					>=6			<12				>=12

Pivot 1 und Pivot 20

letzte Listen erzeugen

1		2										15		20
		>=1										<20

keine Pivots mehr, nur noch einstellige Listen

wieder zusammensetzen

Sortierte Liste

Der Quick Sort hat eine mittlere Zeitkomplexität von $O (n \log n)$ und ist somit schneller als Bubble- und Selection Sort.

Hingegen arbeitet er nicht in-place und hat eine grössere Platzkomplexität, da neue Listen erstellt werden müssen.

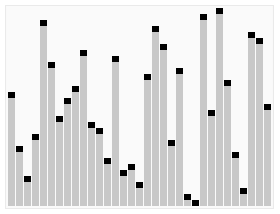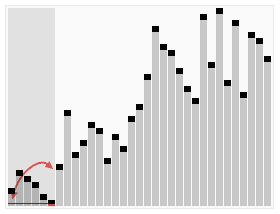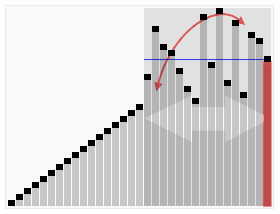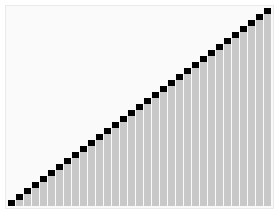
Animation

Wir sehen wie der Quick Sort mit Hilfe des Pivot-Elementes die Liste mehrfach unterteilt und neuen Listen mit kleineren und grösseren Elementen erstellt, um dann auf ihnen genau gleich vorzugehen.

Animation ​

Animation