Algorithmen mit einer polynomialen Laufzeit von $n^2$ oder allgemein $n^k$ skalieren bereits schlecht. Das bedeutet, dass sie bei einem grösseren Input, kaum brauchbar sind, weil sie das Resultat nicht mehr in nützlicher Zeit liefern können. Sie gelten aber immer noch als effizient. Man muss die Input-Länge kontrollieren.

Algorithmen mit exponentieller Laufzeit, also $2^n$ oder $k^n$, werden nicht mehr als effizient bezeichnet. Ihre Komplexität wächst so stark mit steigendem Input, dass sehr bald schon keine Resultate mit vernünftigem Aufwand möglich sind.

«Vergleich Komplexität»

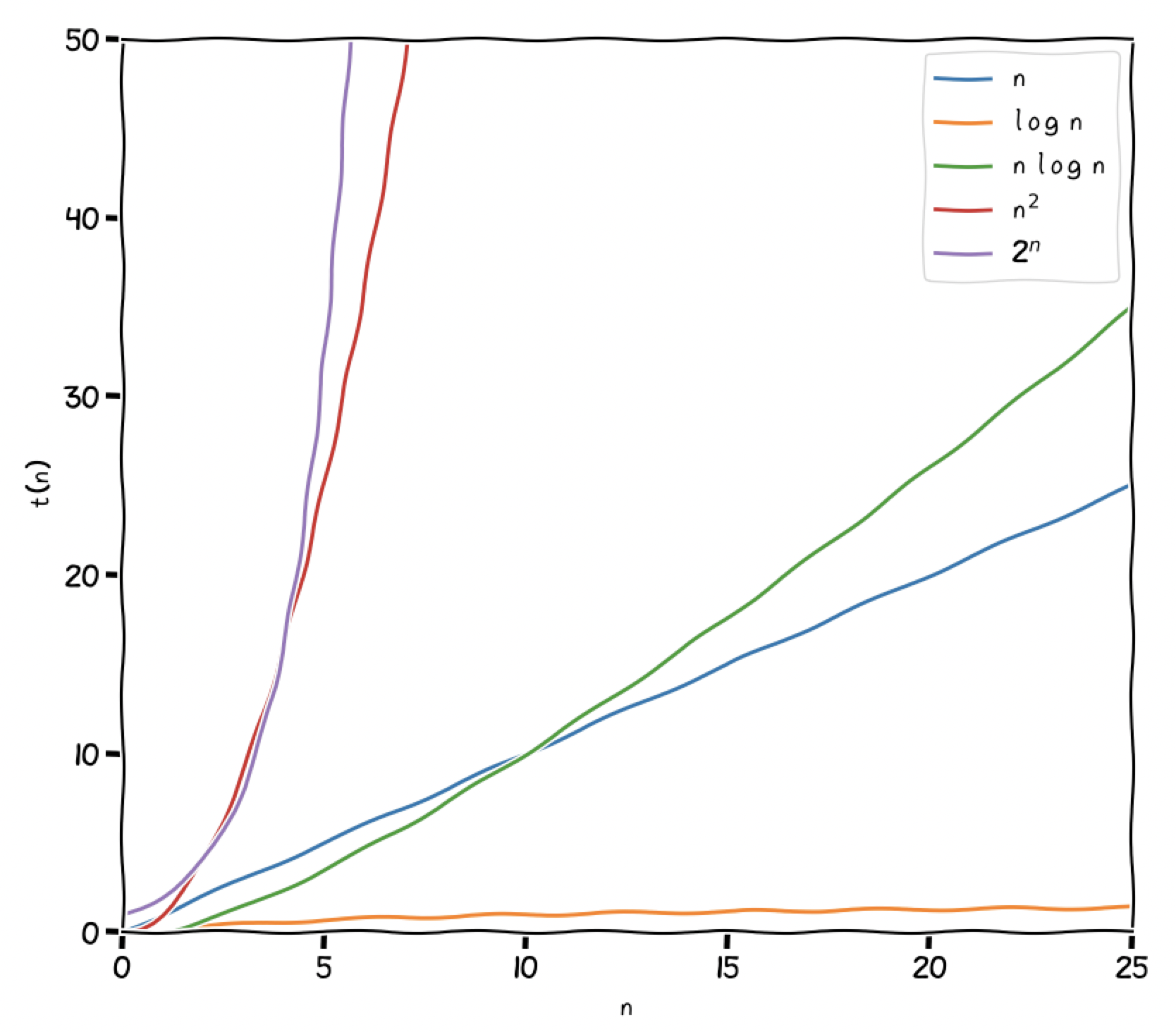
Für viele Probleme der Informatik hat man noch keine effiziente Algorithmen gefunden, also solche mit polynomialer Laufzeit oder besser.

Komplexitätsklasse P

Definition

Die Komplexitätsklasse $\mathcal{P}$ enthält die Probleme, für die eine deterministische Turingmaschine (etwa ein konventioneller Computer) existiert, die das Problem in polynomialer Laufzeit löst.

Komplexitätsklasse NP

Definition

Die Komplexitätsklasse $\mathcal{NP}$ enthält die Probleme, von denen sich in polynomialer Laufzeit mit einer deterministischen Turingmaschine entscheiden lässt, ob eine vorgeschlagene Lösung zutrifft.

P-NP-Problem

Unbekannt ist, ob die beiden Klassen $\mathcal{P}$ und $\mathcal{NP}$ identisch sind, ob also auch die schwersten Probleme der Klasse $\mathcal{NP}$ deterministischen Maschinen effizient lösbar sind.

P-NP-Problem

Beispiele

Faktorisierung

Ein solches Beispiel ist die Faktorisierung einer Zahl in ihre Primfaktoren.

$$\text{z.B. }91=7\ast 13\text{ oder }12=2\ast 2\ast 3$$

Diese Aufgabe scheint einfach, wird aber für sehr grosse Zahlen sehr aufwändig!

Aufgabe: (nicht ernst gemeint)

Wie lauten die beiden Primfaktoren der folgenden 129-stelligen Zahl?

114 381 625 757 888 867 669 235 779 976 146 612 010 218 296 721 242 362 562 561 842 935 706 935 245 733 897 830 597 123 563 958 705 058 989 075 147 599 290 026 879 543 541

Es ist kein polynomiales Faktorisierungsverfahren bekannt – es kann aber auch nicht ausgeschlossen werden, dass es ein solches gibt! Dieses sogenannte P-NP-Problem ist eines der grossen ungelösten Probleme der theoretischen Informatik.

SAT – Erfüllbarkeitsproblem der Aussagenlogik

Das Erfüllbarkeitsproblem der Aussagenlogik (SAT, von englisch satisfiability) ist ein Entscheidungsproblem der theoretischen Informatik. Es beschäftigt sich mit der Frage, ob eine gegebene aussagenlogische Formel $F$ erfüllbar ist. Mit anderen Worten: Existiert eine Belegung der Variablen von $F$ mit den Werten wahr oder falsch, so dass $F$ zu wahr ausgewertet wird?

Beispiel einer solchen aussagelogsichen Formel:

$$F=(A\vee B)\wedge (\mathrm{\neg }A\vee D\vee \mathrm{\neg }E)\wedge (B\vee \mathrm{\neg }D\vee E)$$

Notation wie wir es von Python kennen:

F = (A or C) and (not A or D or not E) and (B or not D or E)

Aufgabe

Finde eine Belegung der boolean Variablen A - E, womit F True ergibt.

SAT gehört zur Komplexitätsklasse NP. Jedes Problem aus NP kann in polynomieller Zeit auf SAT zurückgeführt werden (Polynomialzeitreduktion).

Eine deterministische Turingmaschine kann SAT in exponentieller Zeit entscheiden, zum Beispiel durch das Aufstellen einer Wahrheitstabelle. Es ist kein effizienter Algorithmus für SAT bekannt und es wird allgemein vermutet, dass ein solcher Polynomialzeitalgorithmus nicht existiert. Die Frage, ob SAT in polynomieller Zeit gelöst werden kann, ist äquivalent zum P-NP-Problem.