Mit Hilfe der While-Schleife, können wir Code wiederholt ausführen. Vor jedem Ausführen der Schleife wird eine Bedingung überprüft. Ergibt diese True, dann wird der Schleifeninhalt ausgeführt. Ergibt sie False, dann wird die Schleife beendet und der nachfolgende Code ausgeführt. Der Schleifeninhalt wird durch Einrücken gekennzeichnet.

solange die Bedingung gilt wiederhole…

Syntax

while bedingung:
	#mach etwas

bedingung ist ein Ausdruck oder der Aufruf eines Unterprogramms der True oder False ergibt.

Beispiele/Aufgaben

Aufgabe: feste Anzahl Wiederholungen

Um eine feste Anzahl Wiederholungen zu erreichen, verwenden wir eine Zählvariable die nach jedem Durchlauf erhöht wird:

Zuerst definieren wir eine Zählvariable und setzen sie auf einen Startwert.
Nun können wir eine while-Schleife ausführen: Solange i kleiner als 10 ist wird i ausgegeben. Nicht vergessen: i am Ende der Schleife vergrössern!

i = 0
while i < 10:
	print("hallo", i)
	i = i + 1

Gib alle Ungeraden Zahlen zwischen 0 und 100 aus

Lösung: feste Anzahl Wiederholungen

Mit `while``

i = 0
while i < 100:
	print("hallo", i)
	i = i + 2

Auch korrekt wäre eine for-Schleife mit range:

for i in range(0,100,2):
    print(i)

Beispiel: «zufälliger» Abbruch der Schleife

Wir simulieren Würfelwürfe mit Hilfe von Zufallszahlen. Wir wollen zählen, wie viele Würfe wir brauchen, bis wir eine 6 werfen. Bei einer 6 wird die Schleife abgebrochen und die Anzahl benötigter Würfe ausgegeben:

import random

count = 0
wurf = 0

while wurf < 6:
	wurf = random.randint(1,6)
	count = count + 1
	print(str(count) + ". Wurf:", wurf)

print("Anzahl Würfe bis 6:", count)

Aufgabe: Yatzy

1. Simuliere Würfe mit mehreren Würfeln. Beim Yatzy hat man z.B. 5 Würfel.
2. Wie gross ist die Wahrscheinlichkeit, dass man im ersten Versuch alle 5 gleich hat?

Lösung: Yatzy

1. Wir brauchen 5 Würfel und würfeln mit allen 5 so lange, wie nicht alle gleich sind: (Achte auf die Start-Werte der Würfel!)

import random

count = 0
würfel1 = 1
würfel2 = 2
würfel3 = 3
würfel4 = 4
würfel5 = 5

while not (würfel1 == würfel2 == würfel3 == würfel4 == würfel5):
	würfel1 = random.randint(1,6)
	würfel2 = random.randint(1,6)
	würfel3 = random.randint(1,6)
	würfel4 = random.randint(1,6)
	würfel5 = random.randint(1,6)
	count = count + 1

print("Anzahl Würfe bis Yatzy:", count)
print(würfel1,würfel2,würfel3,würfel4,würfel5)

Alternativ kann man mit einer Endlosschleife und einer Abbruchbedingung mit break in der Schleife drin arbeiten: (dann kann man die Würfel auf 0 initialisieren)

import random

count = 0
würfel1 = 0
würfel2 = 0
würfel3 = 0
würfel4 = 0
würfel5 = 0

while True:
    würfel1 = random.randint(1,6)
    würfel2 = random.randint(1,6)
    würfel3 = random.randint(1,6)
    würfel4 = random.randint(1,6)
    würfel5 = random.randint(1,6)
    count = count + 1
    if würfel1 == würfel2 == würfel3 == würfel4 == würfel5:
        break

print("Anzahl Würfe bis 6:", count)
print(würfel1,würfel2,würfel3,würfel4,würfel5)

2. Wir könnten unser obenstehendes Programm ganz oft ausführen und schauen, wie oft wir im ersten Versuch ein Yatzy würfeln. Das bräuchte aber sehr viel Rechenzeit! Alternativ könnte man schauen, wie oft man im Schnitt Würfeln muss, um ein Yatzy zu erhalten und dann umrechnen. Bei genügend vielen Versuchen, sollte unser Wert die berechnete Wahrscheinlichkeit annähern:

$$(\frac{1}{6}{)}^5=(\frac{1}{7776})=0.0001286$$

Zusatzaufgabe

Zusatzaufgabe: «𝛑 mit Monte-Carlo»

Versuche eine möglichst genaue Näherung für 𝛑 mit der unten beschriebenen Monte-Carlo-Methode zu bestimmen.
Als Erweiterung kannst du den Versuch auch grafisch darstellen.

Tipp: 𝛑 mit Monte-Carlo

Die Formel zur Berechnung der Fläche eines Kreises, beinhaltet 𝛑. Wir verteilen Punkte zufällig auf eine Fläche, die zum Teil von einem Kreis bedeckt ist. Nun stehen die Anzahl «Treffer» auf den Kreis im Verhältnis zu der Fläche des Kreises. So können wir 𝛑 statistisch bestimmen.

Zur Einfachheit schauen wir einen Viertelkreis mit Radius 1 an und verteilen die Punkte zufällig im umgebenden Quadrat:

PI statistisch^[1]

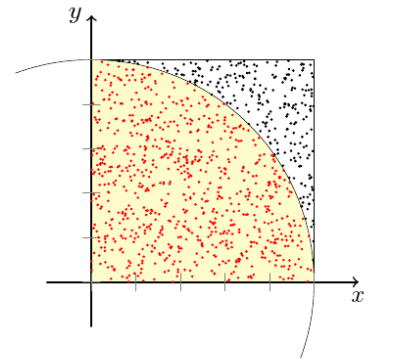
Fläche des Quadrates:

$$A_Q=r^2=1$$

Fläche des Viertelkreises:

$$A_K=\frac{r^2\cdot \pi }{4}=\frac{\pi }{4}$$

Die Wahrscheinlichkeiten, dass ein zufällig gewählter Punkt innerhalb des Viertelkreises liegt ($\text{Treffer}$), verglichen zu innerhalb des Quadrates ($\text{Versuche}$), verhalten sich gleich, wie die Flächen:

$$\frac{\text{Treffer}}{\text{Versuche}}=\frac{A_K}{A_Q}=\frac{r^2\cdot \pi /4}{r^2}=\frac{\pi }{4}$$

Wenn wir dann noch nach $\pi$ auflösen, ergibt dies:

$$\pi =4\cdot \frac{\text{Treffer}}{\text{Versuche}}$$

---

1. Springob via Wikimedia ↩︎