Bäume und Baumsuche | EF Informatik 2021

Die Datenstruktur «Baum» trifft man in der Informatik immer wieder an. So stellt z.B. ein hierarchisches Dateisystem mit Ordner, Unterordner und Dateien eine Baumstruktur dar.

Im Gegensatz zum «normalen» Baum, der in den Himmel wächst, werden die Baumstrukturen meistens nach unten dargestellt:

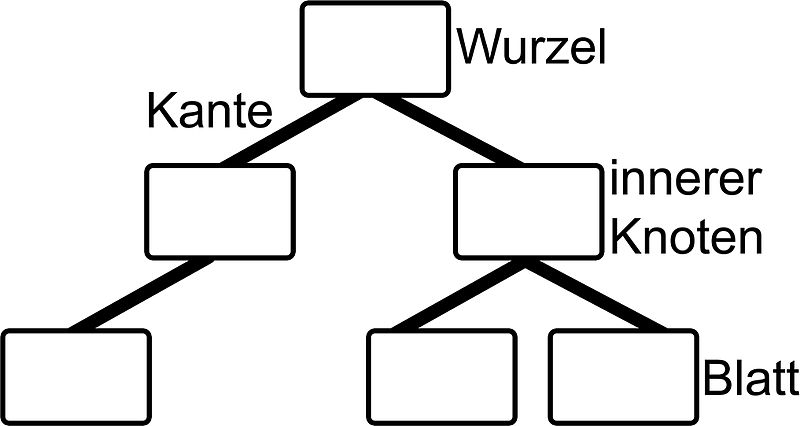
Ein Baum besteht aus Knoten (engl. Nodes) – das sind die Start-, End- und Verzweigungspunkte und Kanten (engl. Edges) – das sind die Verbindungen zwischen den Knoten. Dem obersten Knoten sagt man auch Wurzel (engl. root) und den Endknoten – dort wo keine weiteren Knoten mehr kommen – sagt man Blätter (engl. leaves).

# Suche im Baum

Zwei wichtige Möglichkeiten sind die Tiefen- und die Breitensuche. Bei der Breitensuche wird der Baum Ebene für Ebene durchsucht, während bei der Tiefensuche von der Wurzel her so tief wie möglich entlang eines Pfads vorgedrungen wird, bevor ein anderer Ast ausprobiert wird.

Aufgabe

Zeichne in den folgenden Baum mit verschiedenen Farben den Suchpfad ein für Tiefensuche und Breitensuche:

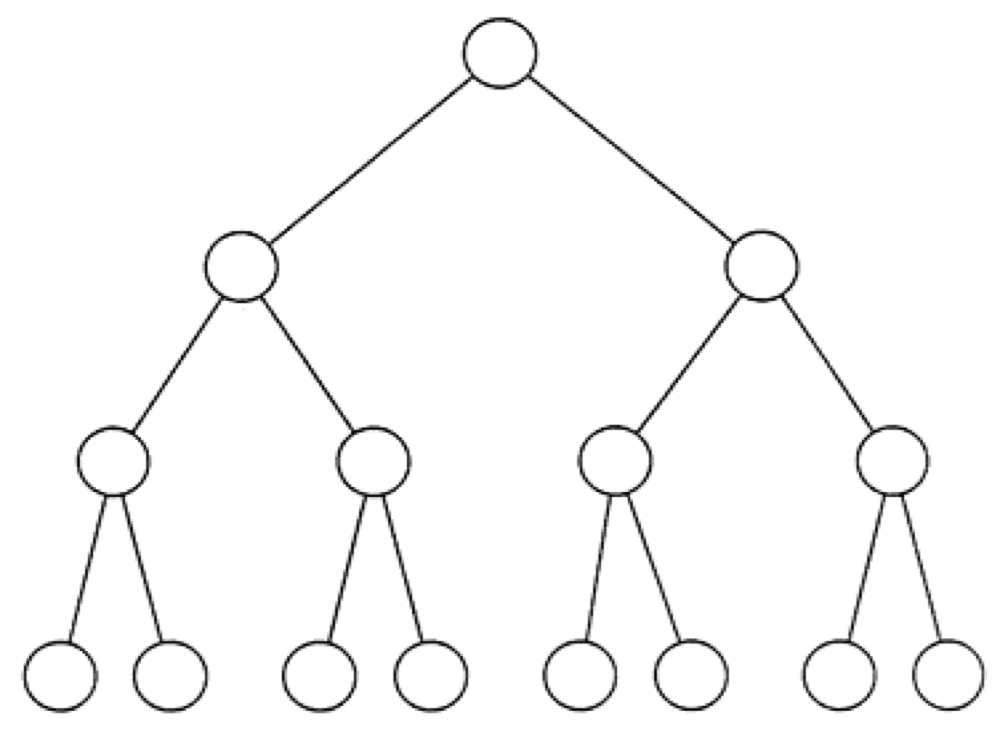
# Vorbereitung

nach Jens Gallenbacher: Abenteuer Informatik

# Ausgangskarte

Als Beispiel wollen wir einen Weg auf einer Karte finden: Es geht von Imstadt nach Lupera.

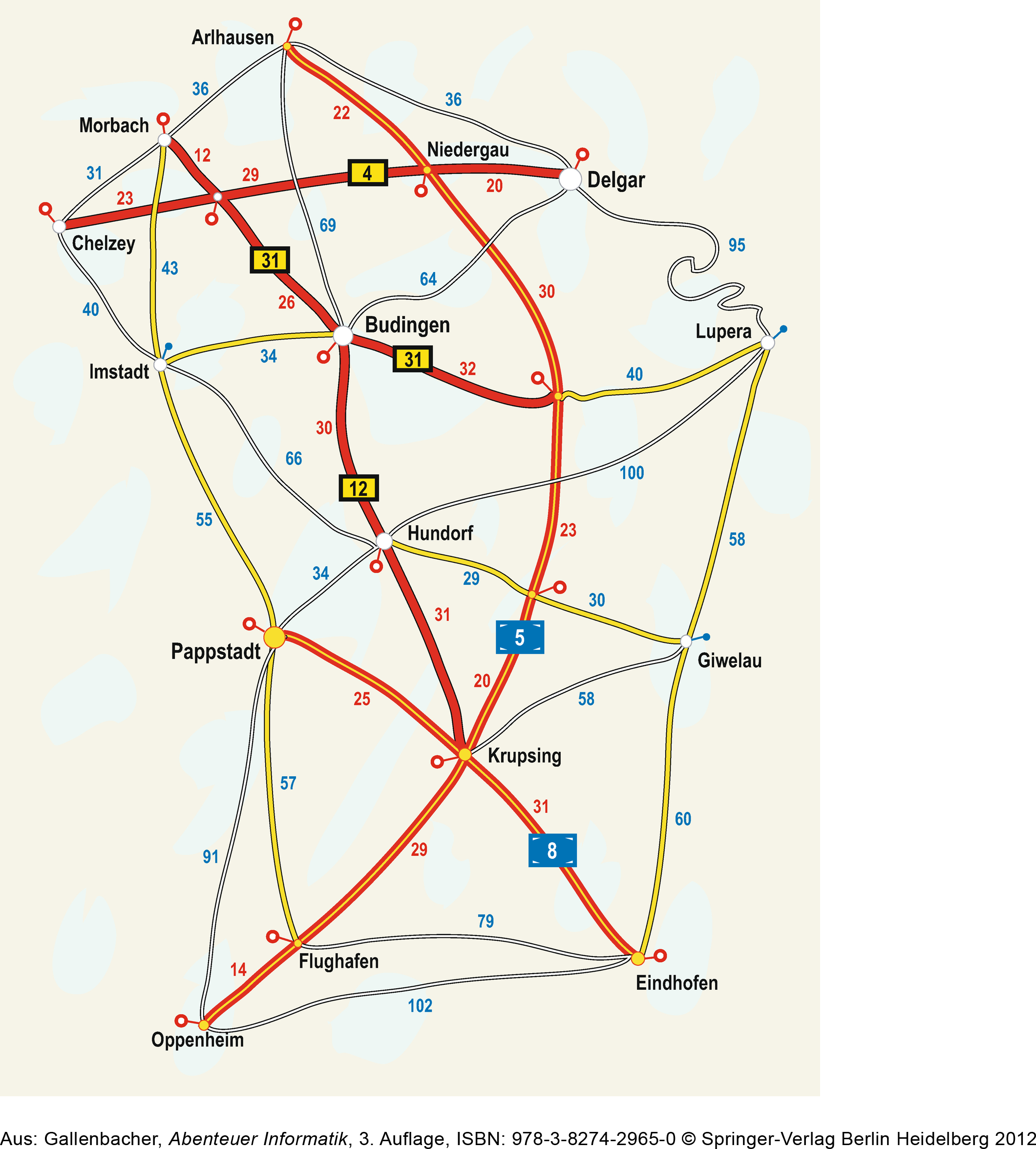
# Schritt 1

Zuerst einmal überlegen wir uns, was denn für die Aufgabe überhaupt wichtig ist. Dabei vereinfachen wir die Karte:

Aus den Städten werden «Knoten» mit einem einzelnen, aber eindeutigen Buchstaben
Kreuzungen werden zu «Knoten»
Strassen werden zu einheitlichen «Kanten» (wir vernachlässigen den Strassentyp)
Die Distanzen bleiben erhalten und werden den Kanten zugewiesen

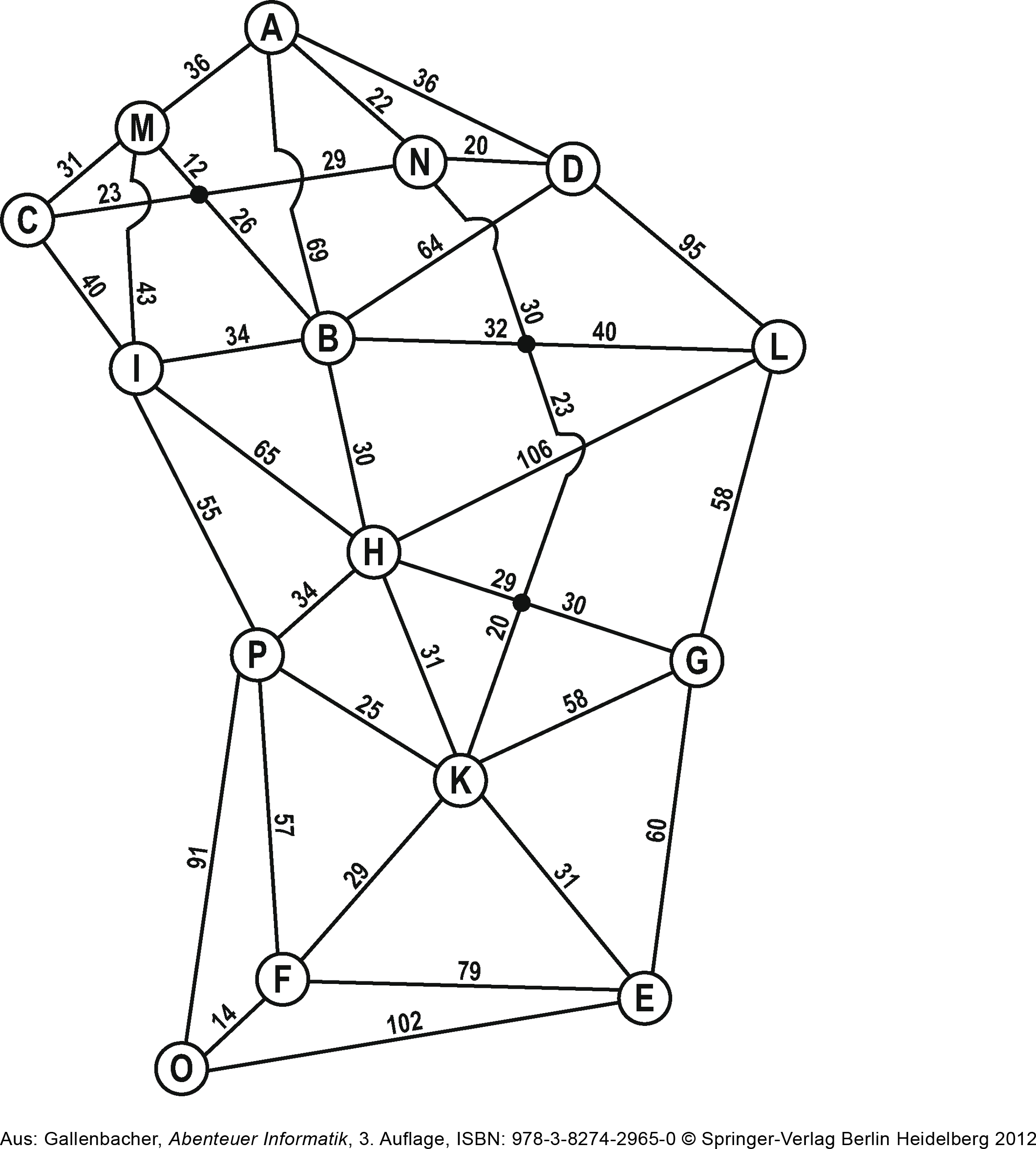
# Schritt 2

Wir können weiter vereinfachen:

Kreuzung-Knoten werden gleich behandelt wie Städte: Sie erhalten einen Buchstaben der noch nicht vergeben ist.
Kanten können gerade dargestellt werden: Dort wo sich zwei Kanten kreuzen gibt es keine Kreuzung!

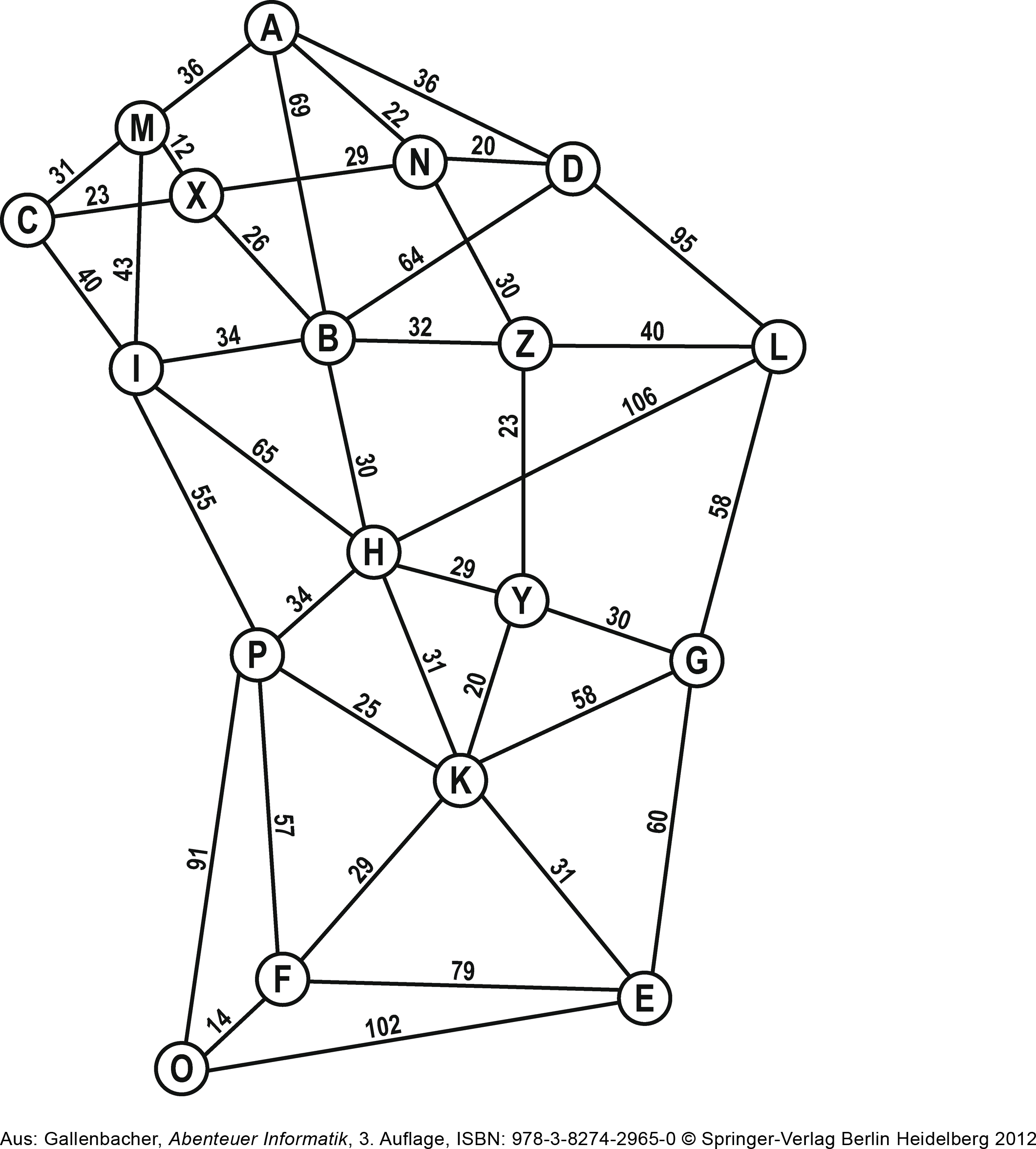
# Endergebnis

Was wir nun erhalten ist ein Gewichteter Graph:
Ein Graph besteht aus Kanten und Knoten. Bei einem gewichteten Graphen hat zusätzlich jede Kante ein Gewicht – bei uns die Länge der Strasse welcher durch die Kante dargestellt wird. Im Gegensatz zur Baumstruktur, darf ein Graph auch Loops beinhalten. («Rundfahrten» sind erlaubt.)

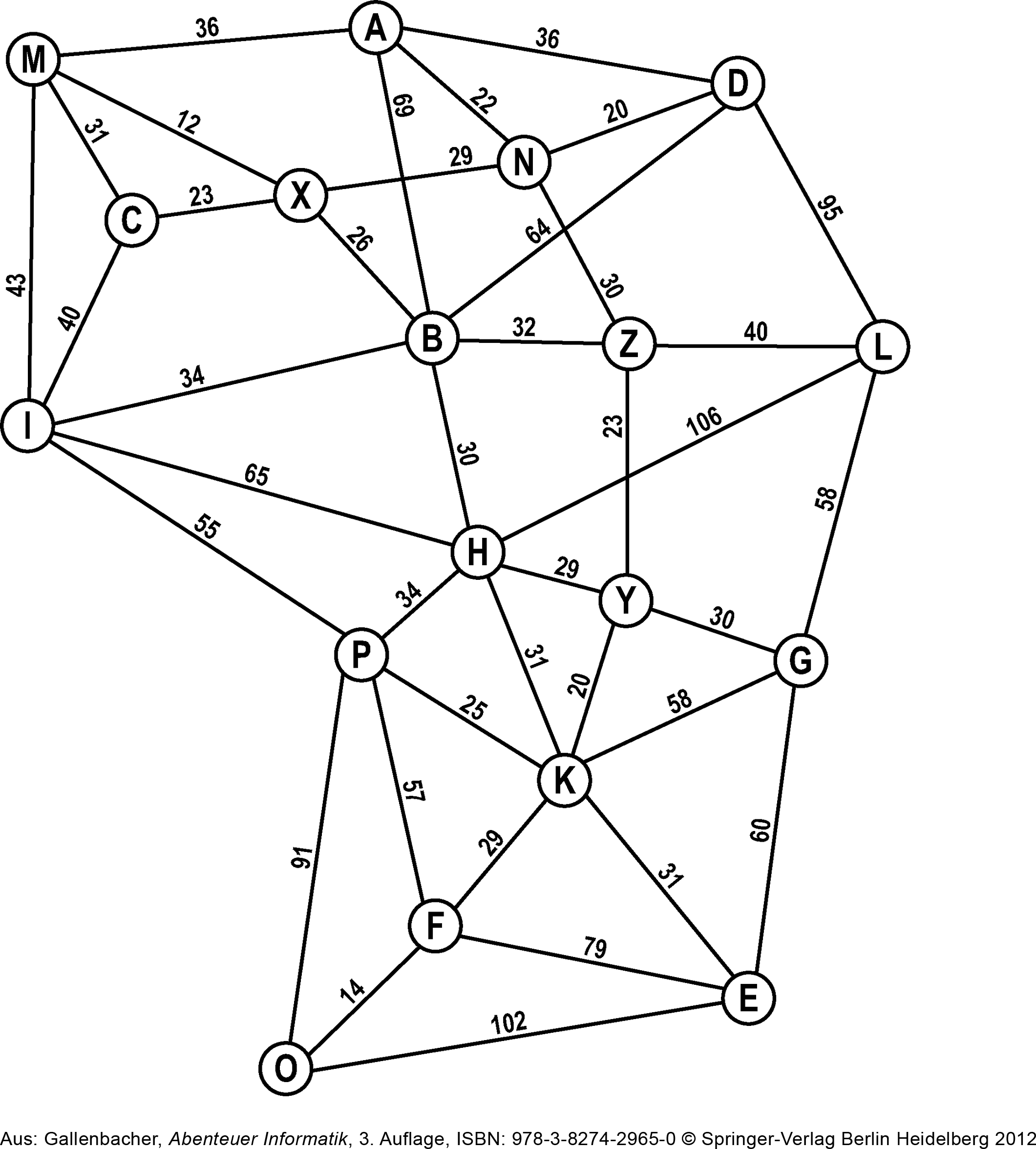
Diesen Graphen können wir nun verwenden, um automatisiert einen Weg – oder sogar den kürzesten Weg zwischen zwei Ortschaften zu finden.

Prinzip der Informatik: «Abstraktion»

Wir vereinfachen, lassen alles nicht wichtige Weg – damit wir das Problem mit dem Computer darstellen und lösen können.

# Breitensuche

Bei der Breitensuche gehen wir – salopp gesagt – in alle Richtungen gleich schnell. Dabei werden etwaige Gewichte zwischen den Knoten ignoriert. Wir werden also einen Weg finden, aber nicht zwingend den Kürzesten!

Für die Suche brauchen wir zwei Listen, womit wir unseren Suchfortschritt festhalten:

Closed-List: Hier werden alle abgehandelten Knoten aufgelistet
Open-List: Hier werden alle bekannten Knoten welche als nächste Kandidaten in Frage kommen aufgeführt

# Vorbereitung

Zu Beginn ist die Closed-List leer. Der Startknoten kommt auf die Open-List:

Closed-List: –
  Open-List: I

# Schritt 1

Wir nehmen den ersten Knoten von der Open-List – das ist Ⓘ – und besuchen alle Nachbarn. Diese werden der Open-List angehängt. Der Knoten Ⓘ gilt jetzt als besucht: Er wird von der Open-List gestrichen und kommt auf die Closed-List.

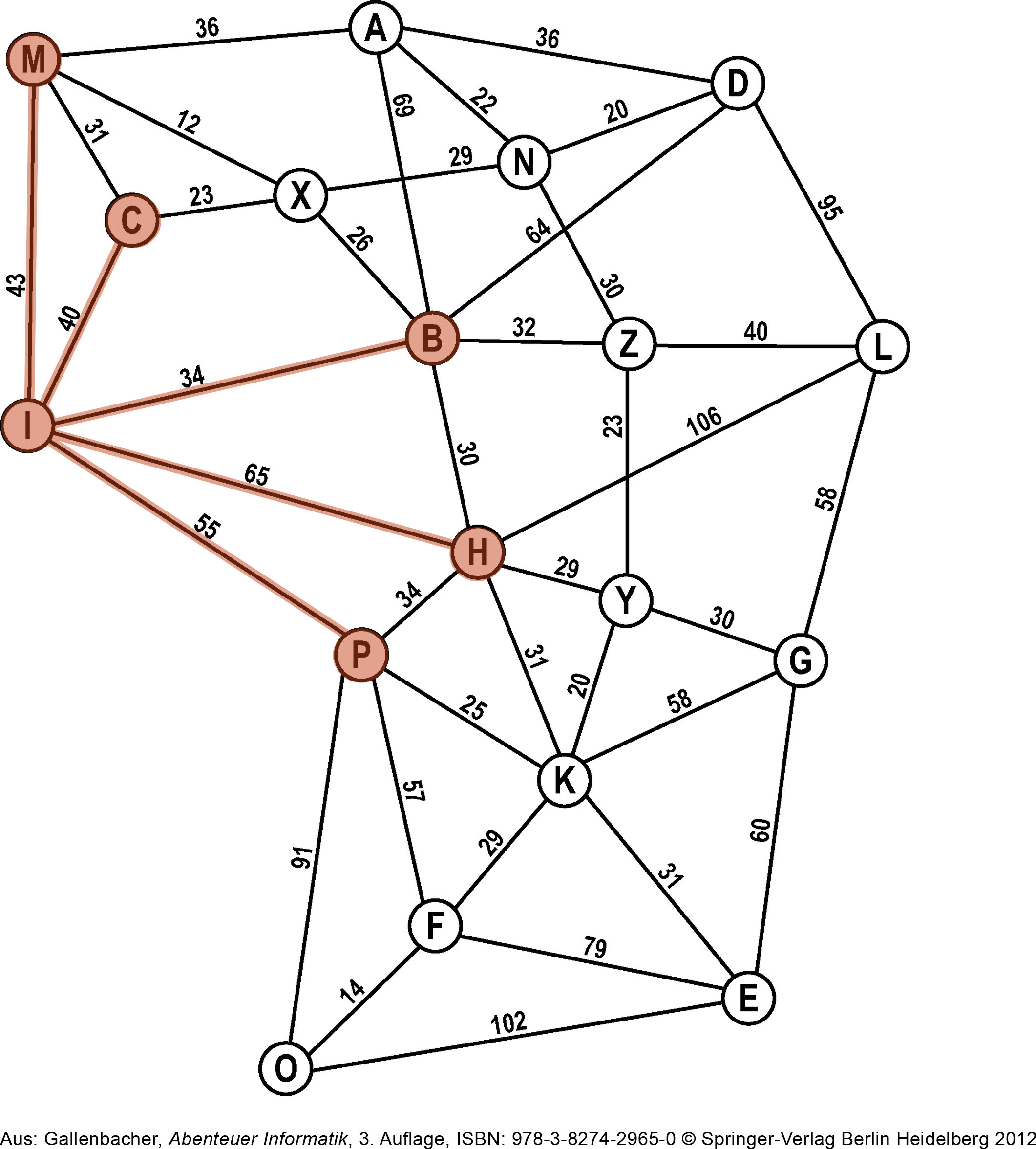
Closed-List: I
  Open-List: M, C, B, H, P

# Schritt 2

Nun besuchen wir wiederum den ersten Knoten auf der Open-List, nämlich Ⓜ. Die Nachbarn Ⓐ und Ⓧ kommen zuhinterst auf die Open-List. Der Nachbar Ⓒ ist bereits auf einer Liste, d.h. wir haben bereits einen Weg zu Ⓒ gefunden. Die Kante zwischen Ⓜ und Ⓒ wird entfernt. (Wir wollen am Schluss zu jedem Knoten nur genau einen Weg haben.)
Ⓜ kommt auf die Closed-List.

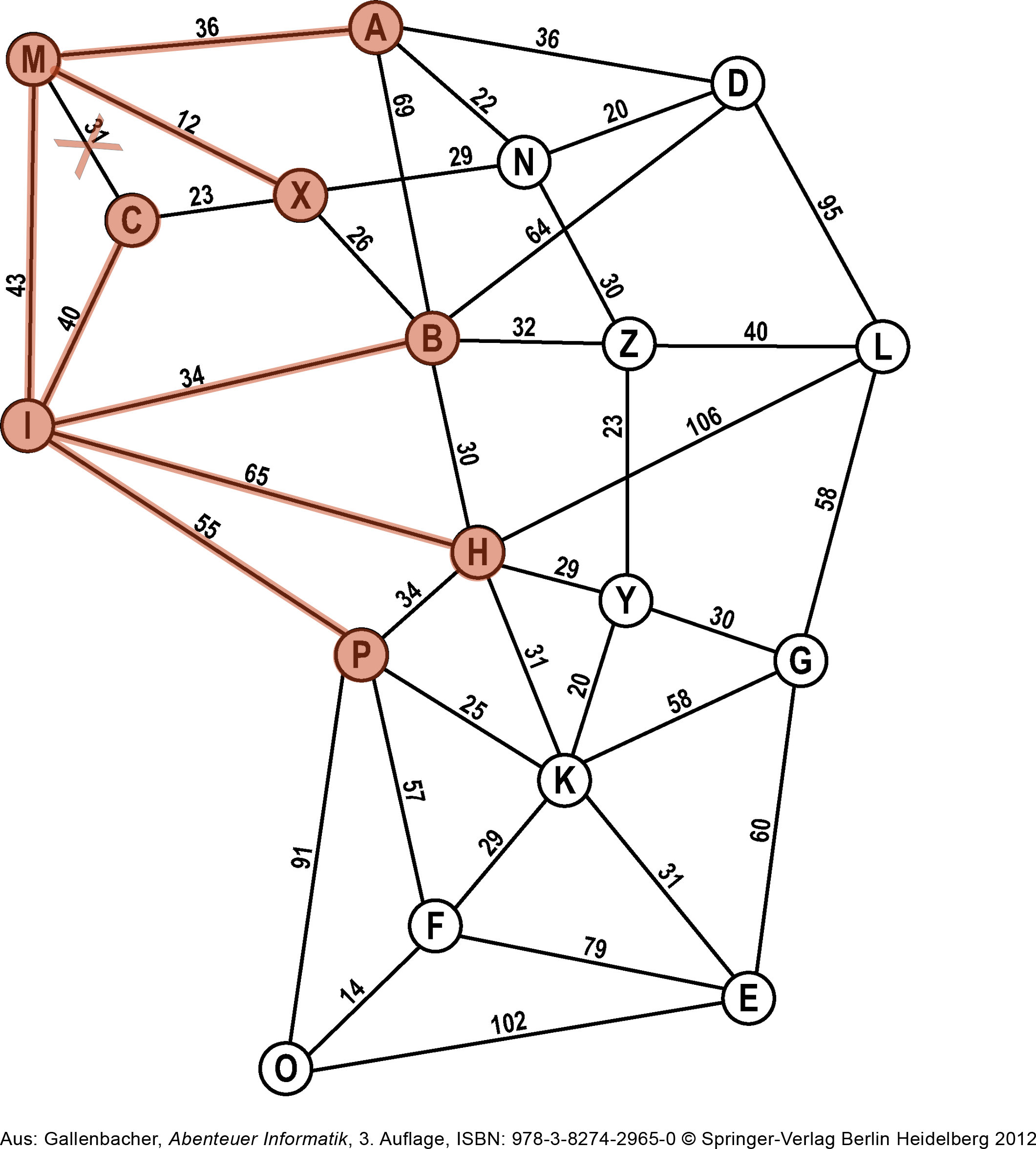
Closed-List: I, M
  Open-List: C, B, H, P, A, X

# Schritt 3

Erneut gehen wir zum ersten Knoten auf der Open-List, also Ⓒ, und schauen uns dessen Nachbarn an: Ⓜ und Ⓧ sind bereites bekannt.
Ⓒ kommt auf die Closed-List.

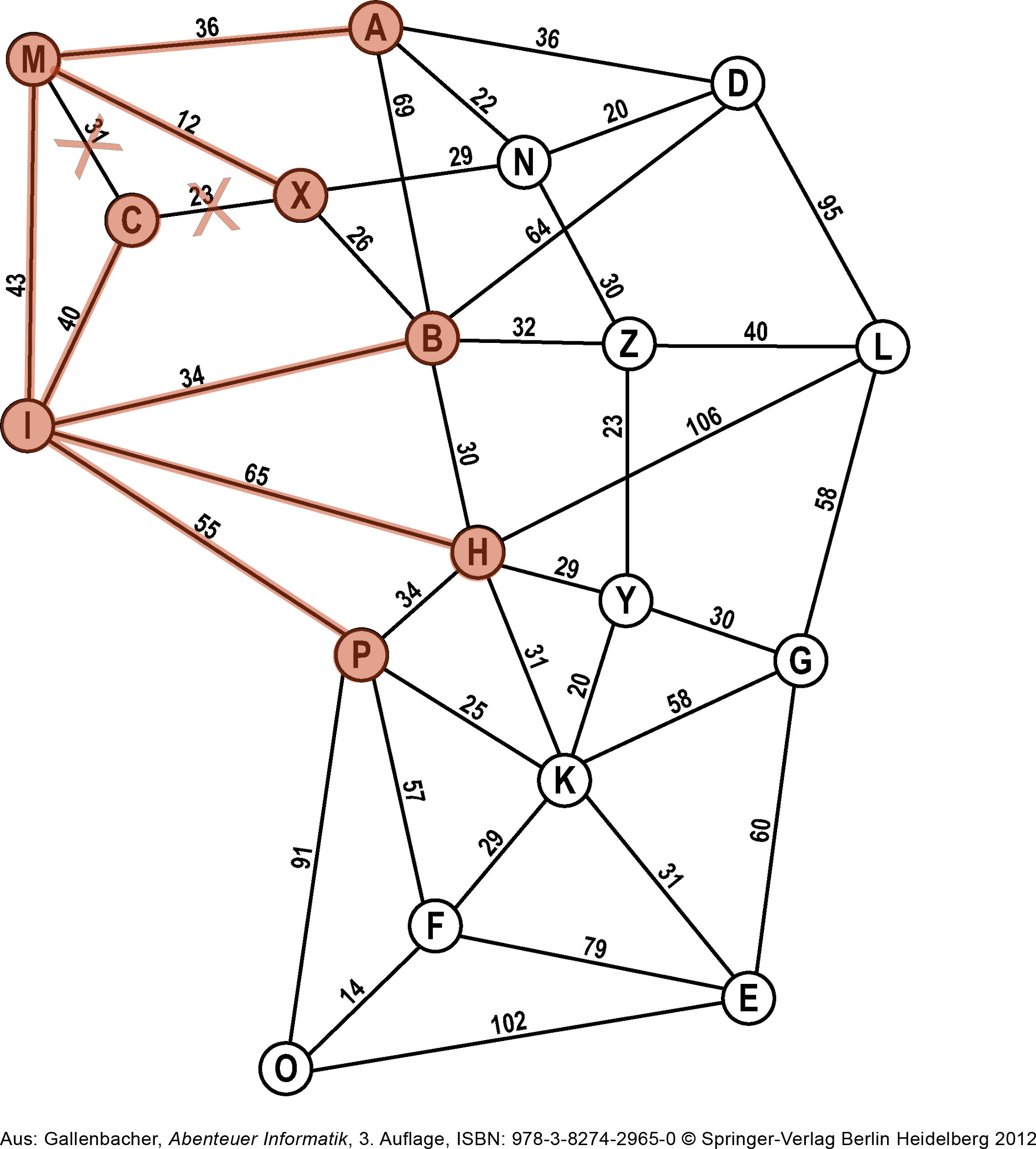
Closed-List: I, M, C
  Open-List: B, H, P, A, X

# Schritt 4

Jetzt sind die Nachbarn von Ⓑ dran: Ⓓ kommt auf die Open-List, ebenso Ⓩ. Den Weg zu Ⓗ haben wir bereits gefunden. Wir können dies Kante also streichen.
Ⓑ kommt auf die Closed-List.

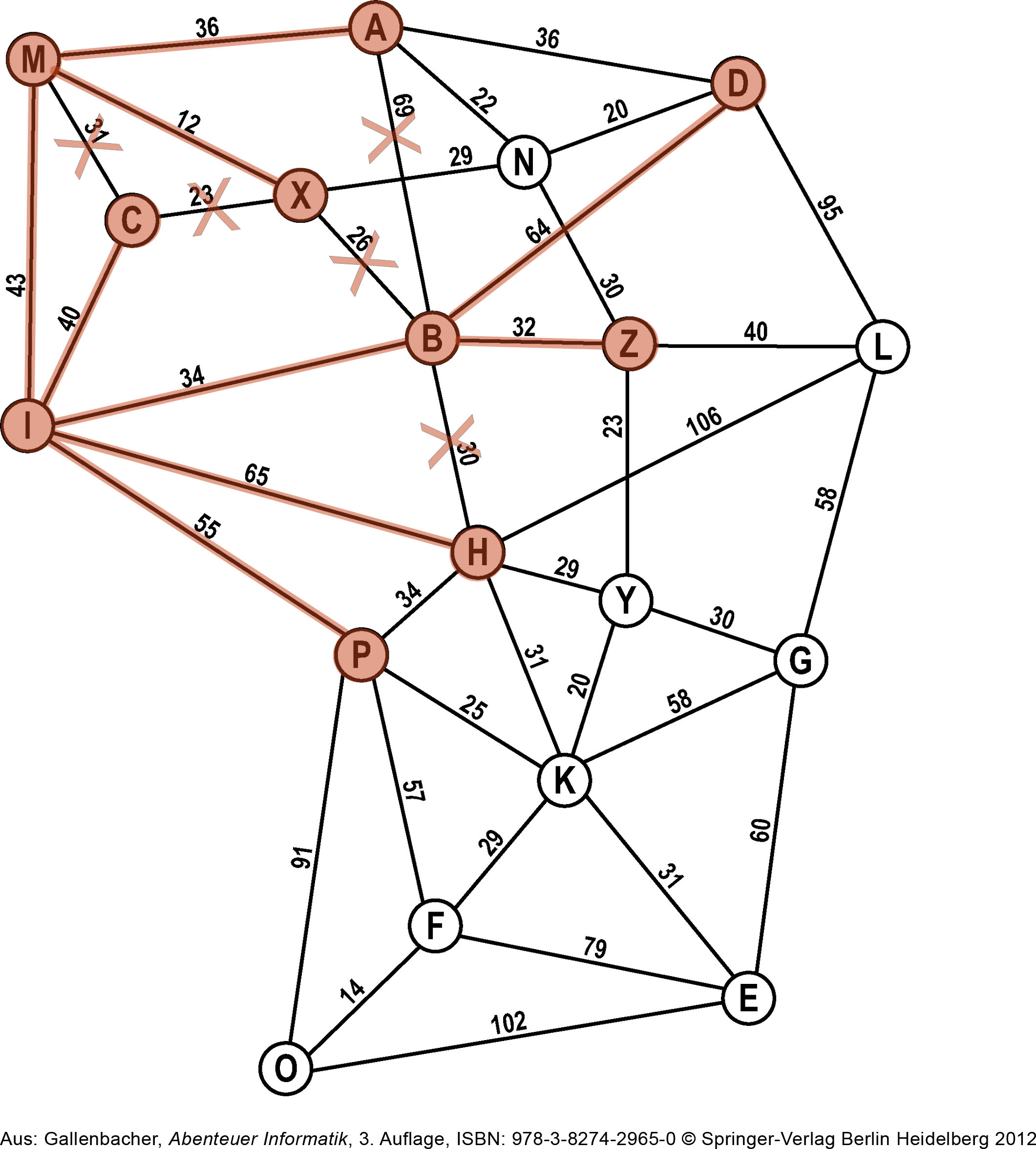
Closed-List: I, M, C, B
  Open-List: H, P, A, X, D, Z

# Schritt 5

Der nächste Knoten auf der Open-List ist Ⓗ. Wir fügen die noch nicht besuchten Nachbarn von Ⓗ zur Open-List hinzu. Es sind dies Ⓛ, Ⓨ und Ⓚ. Ⓛ ist unser gesuchtes Ziel: wir haben also einen Weg von Ⓘ nach Ⓛ gefunden, und zwar über Ⓗ. Ⓗ kommt auf die Closed-List und wir brechen den Algorithmus ab.

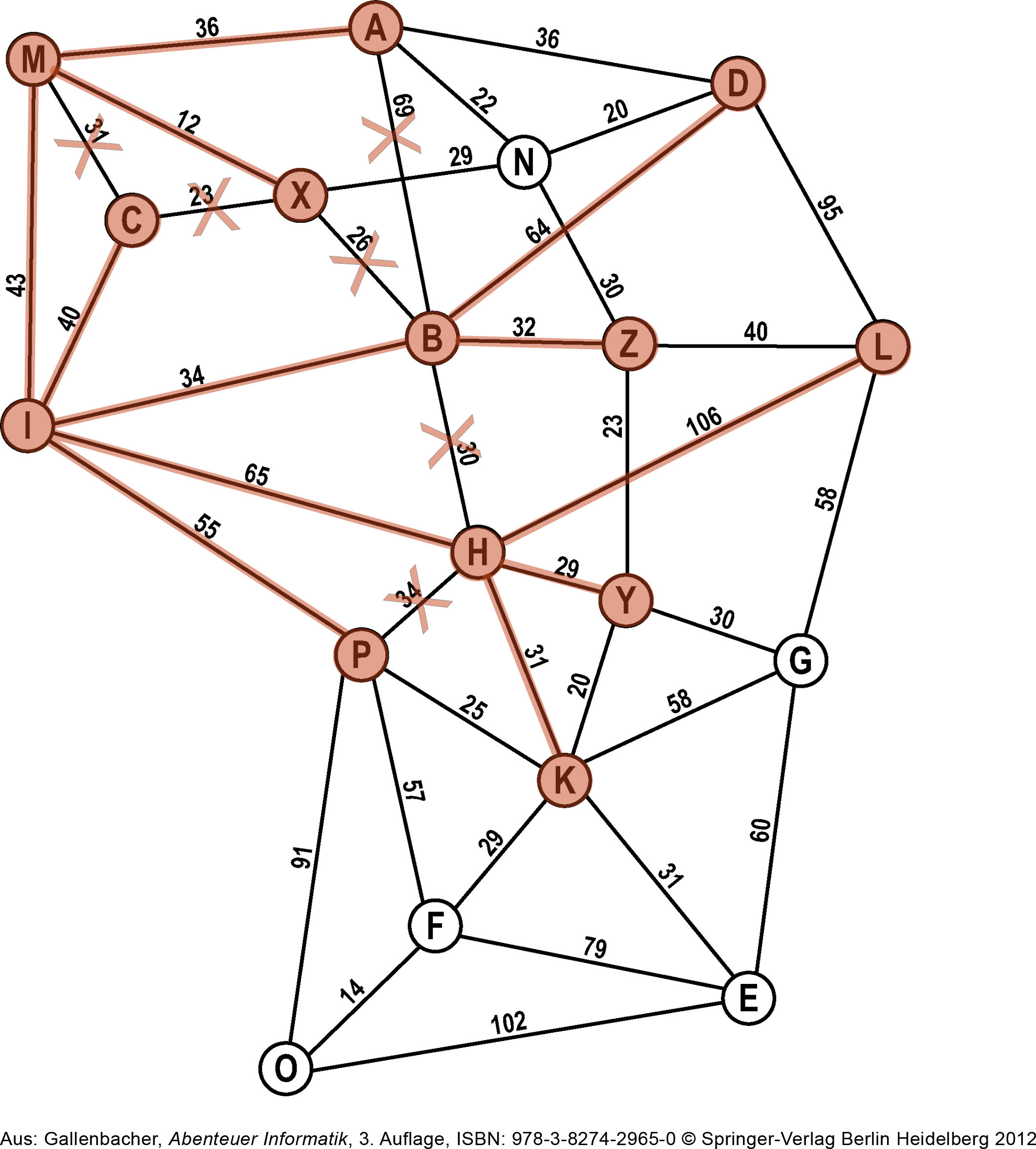
Closed-List: I, M, C, B, H
  Open-List: P, A, X, D, Z, L, Y, K

# Ergebnis

Die roten Linien und Knoten im Graphen stellen einen Baum dar. Wenn wir die Knoten nun etwas umpositionieren erhalten wir den folgenden erforschten Baum:

Dieser Baum zeigt zu jedem erforschten Knoten genau einen Weg vom Startknoten aus. Da wir den Algorithmus abgebrochen haben, sobald wir den Zielknoten gefunden haben, sind nicht alle Knoten aufgelistet. Aber wir finden den gesuchten Weg zum Zielknoten.

Wir zeichnen nun noch mit Pfeilen die Reihenfolge ein in welcher wir diese Knoten «durchsucht» haben:

Diese Art der Baumsuche nennt man Breitensuche.

Aufgabe

Führe selbst eine Breitensuche aus: Finde den Weg in umgekehrter Richtung, also vom Knoten Ⓛ zum Knoten Ⓘ.

Zeichne dein Fortschritt analog zum Beispiel im Graphen auf
Führe daneben eine Open- und eine Closed-List

Aufgabe

Könnten wir diese Aufgabe auch mit einer Tiefensuche bewältigen?
Überlegt zu zweit ob und wie das möglich wäre.

# Ameisen

nach Jens Gallenbacher: Abenteuer Informatik

# Ameisen

Die Ameisen starten gleichzeitig im Startknoten. In alle Richtungen schwärmen sie gleich schnell aus:

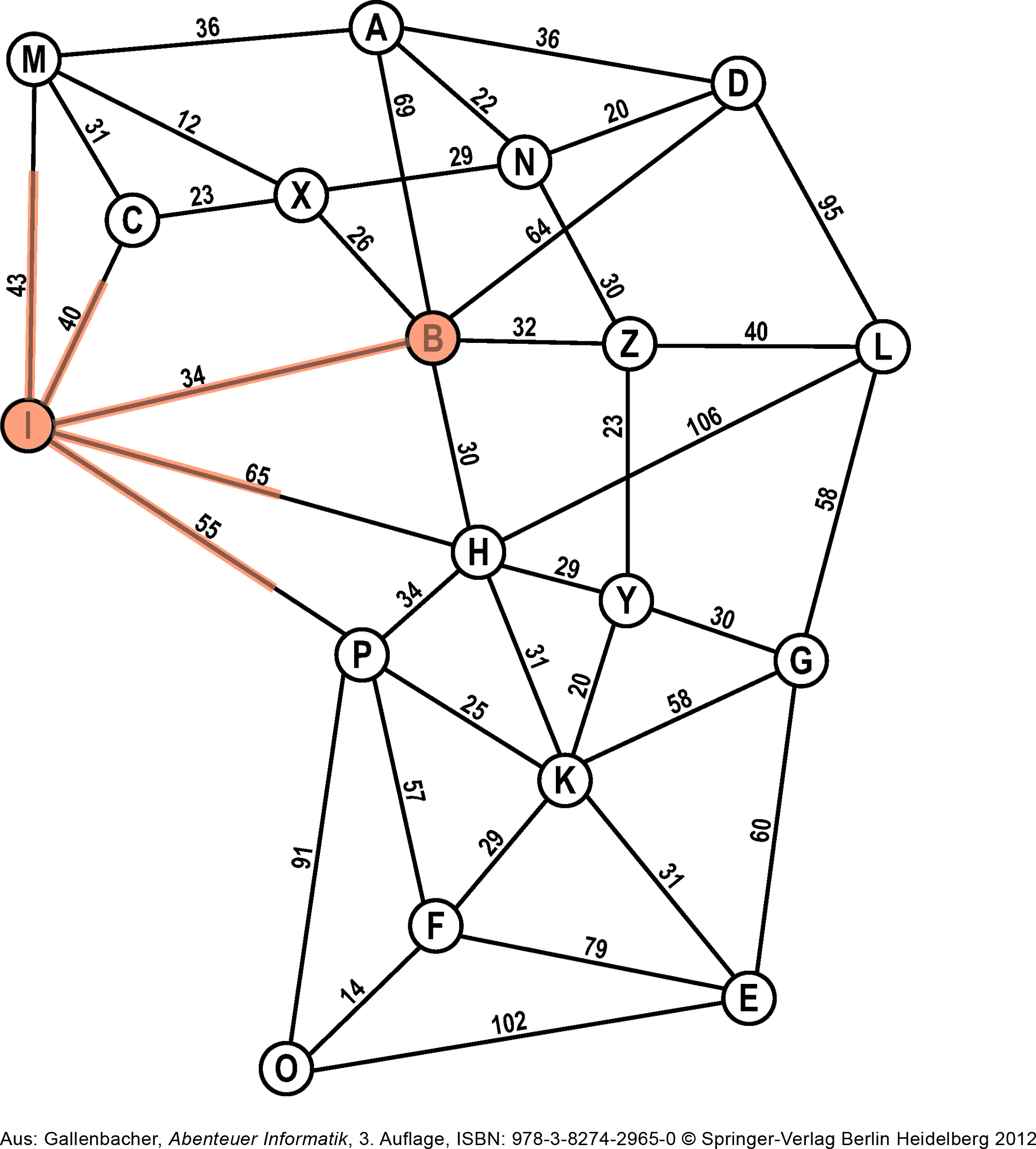
Erreichen Ameisen einen ersten Nachbarknoten, so teilen sie sich sogleich und folgen allen weiteren Verzweigungen, immer noch im genau gleichen Tempo.

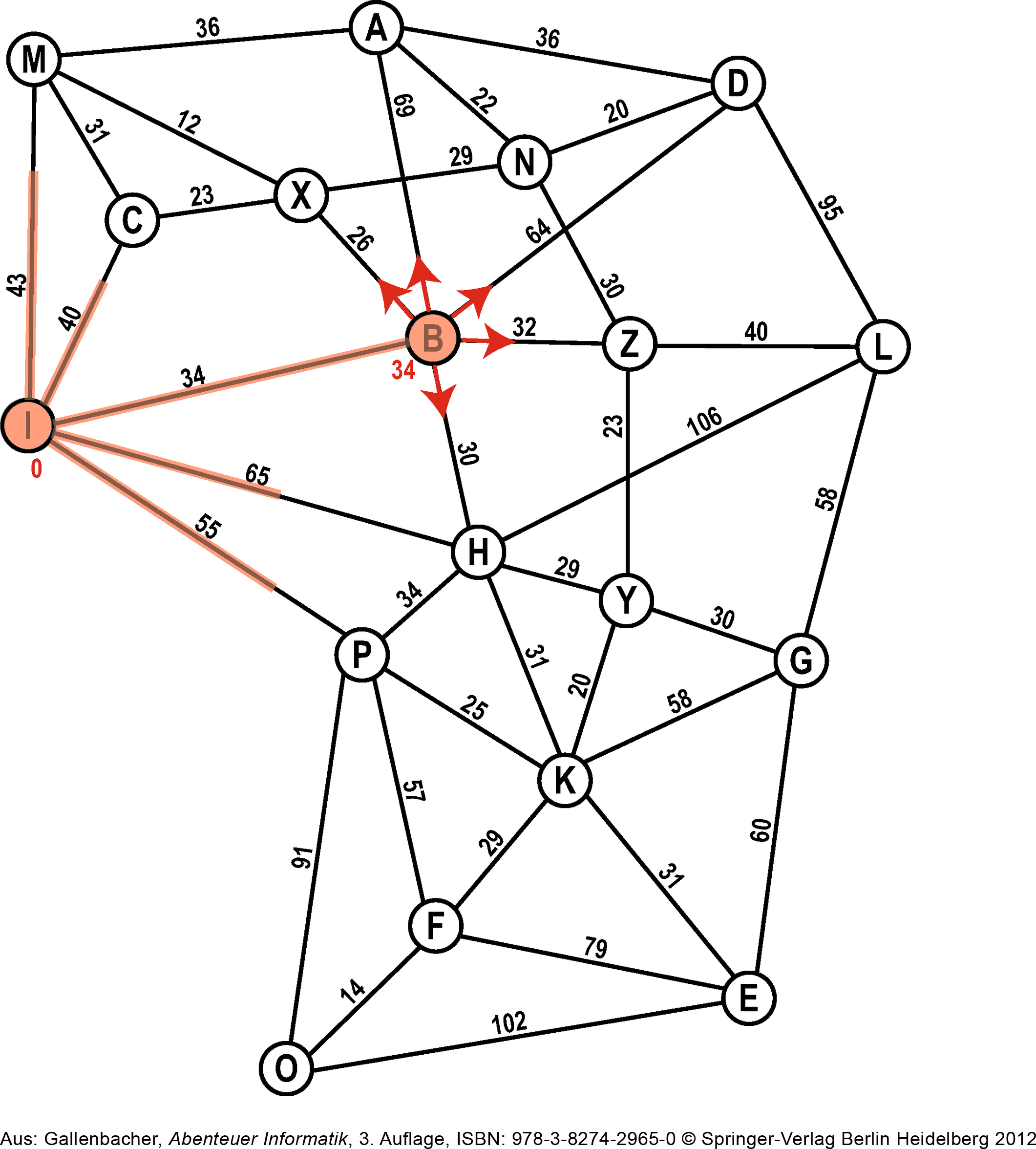
Dasselbe passiert nun bei verschiednen Knoten. Teilweise marschieren Ameisen auf der selben Kante aufeinander zu.

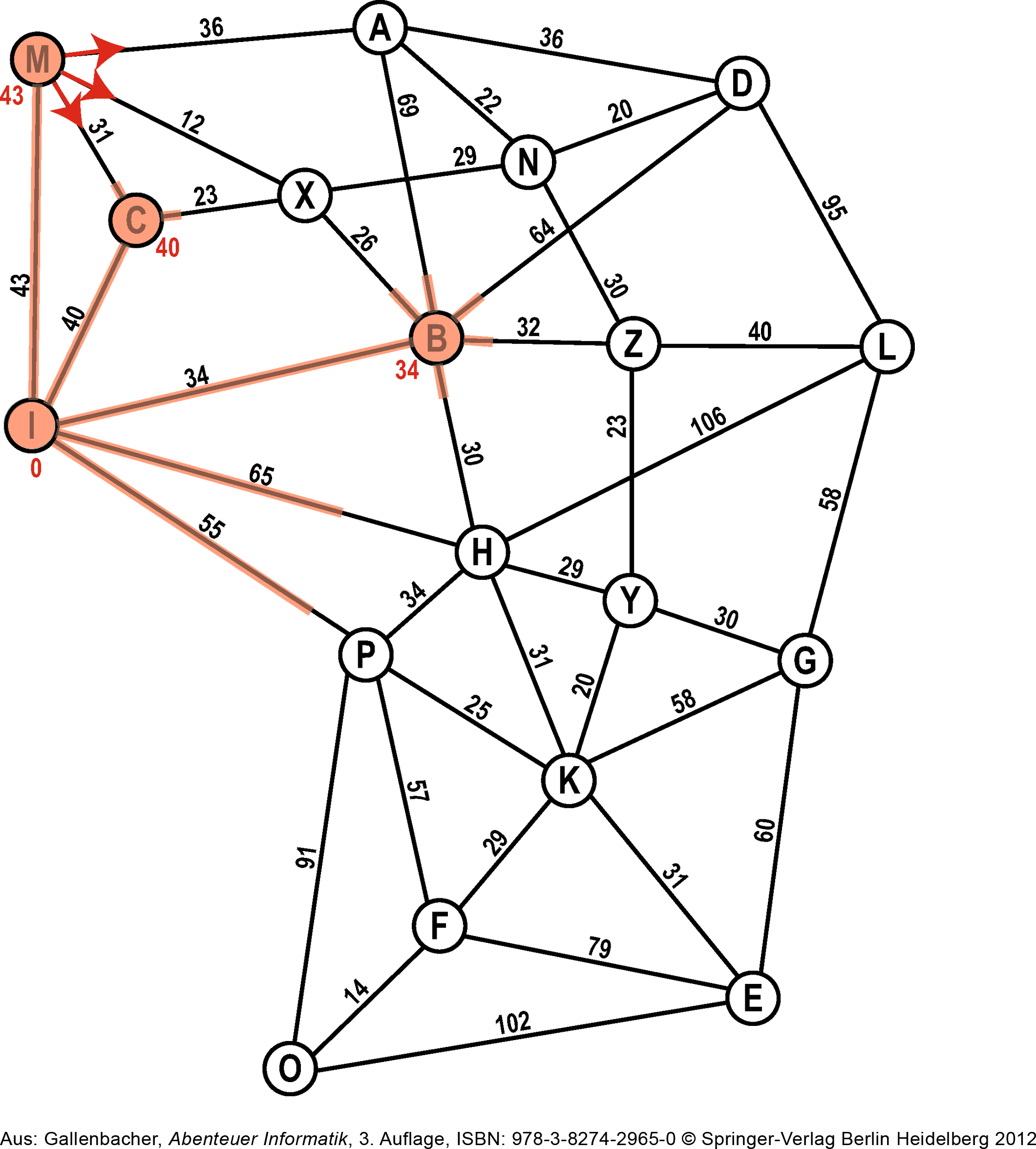
Treffen sich aus unterschiedlicher Richtung kommende Ameisen auf einer Kante, so wird diese Kante entfernt: Man weiss dass die beiden Knoten, von wo die Ameisen aus auf diese Kante gekommen sind, bereits entdeckt sind.

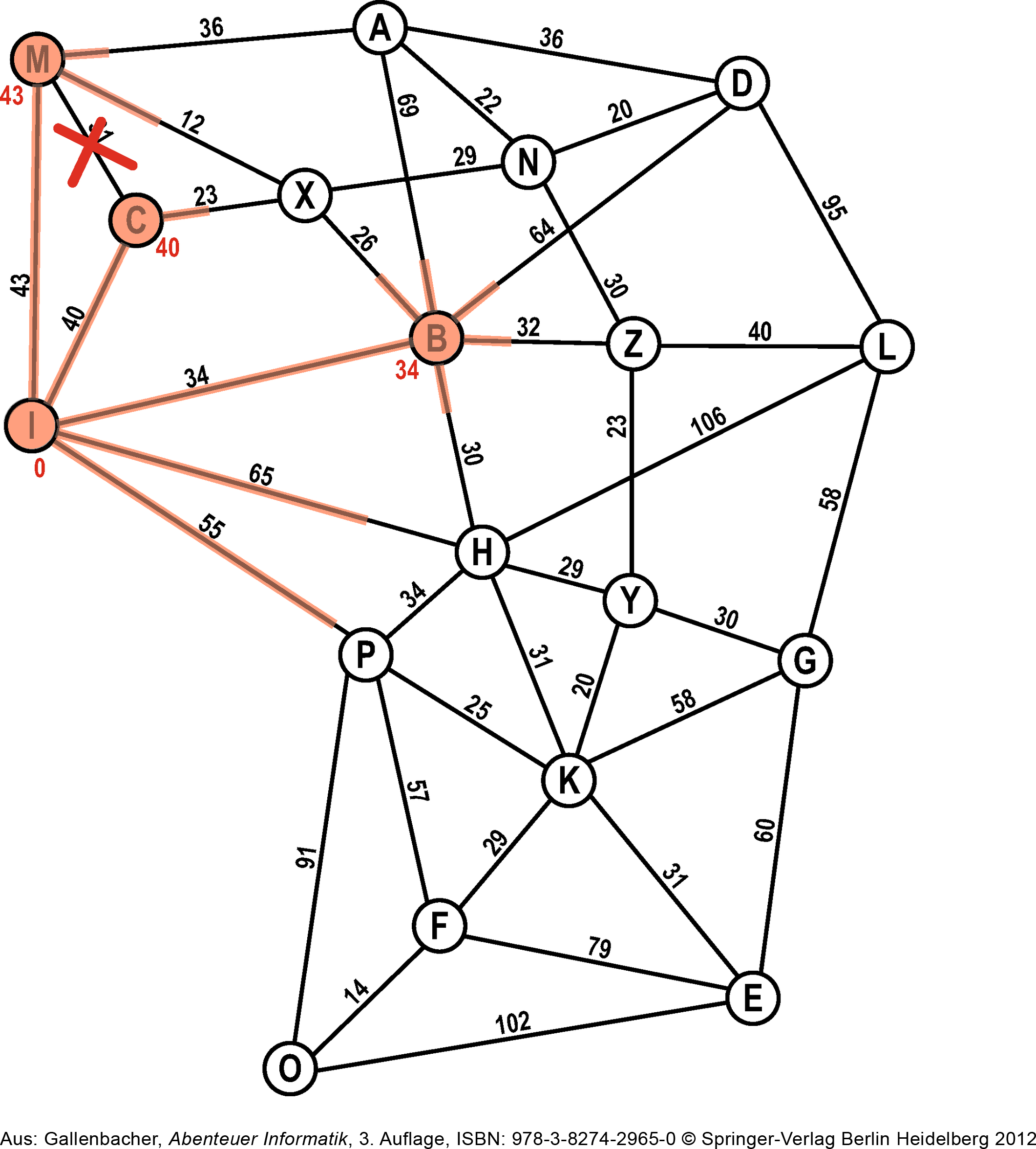
So geht das Entdecken weiter: Bei neuen Knoten teilen sich die Ameisen, bei Kanten begegnen sie sich.

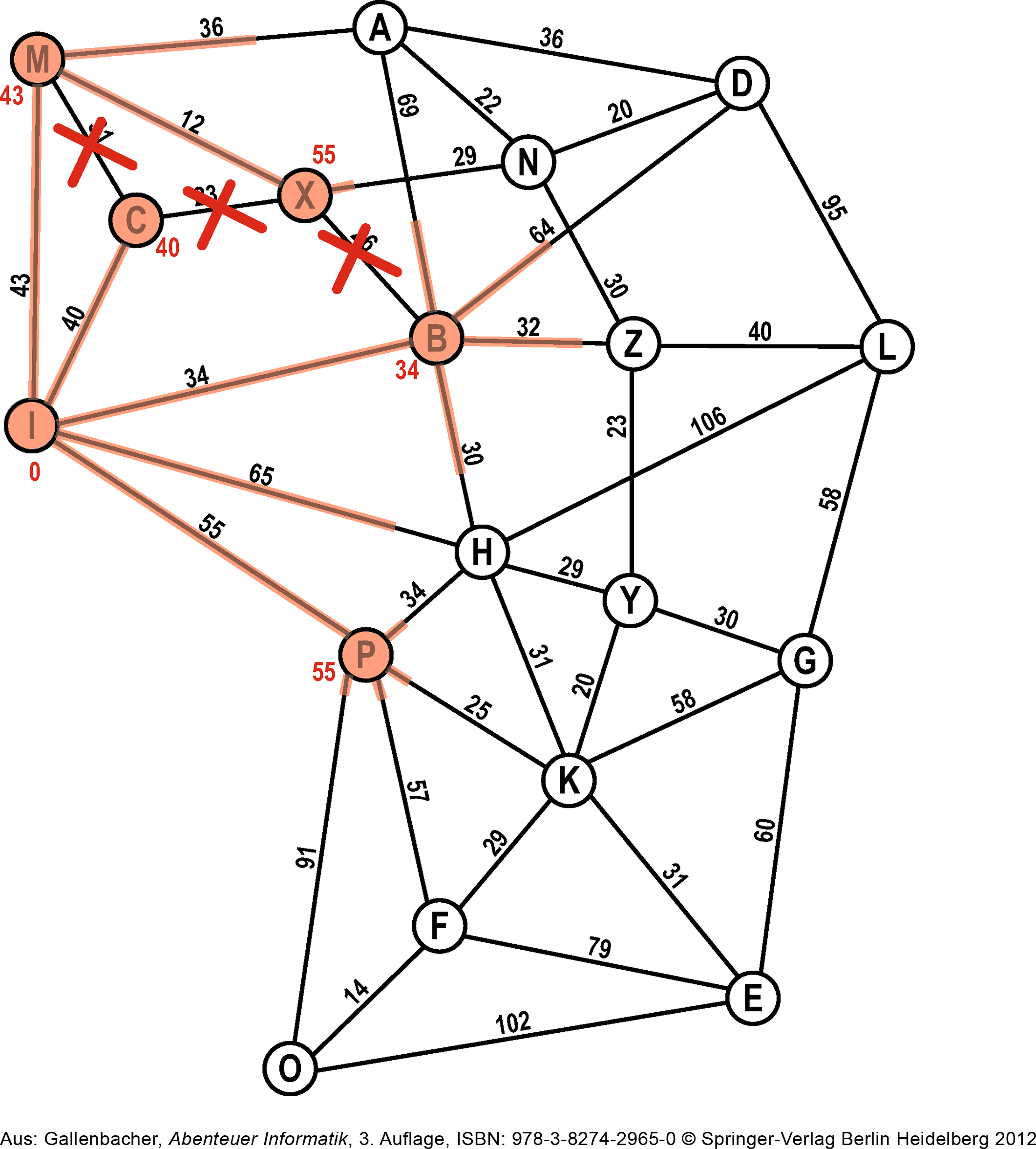
Schlussendlich ist jeder Knoten von Ameisen entdeckt worden. Und zwar immer auf dem schnellsten Weg vom Startknoten aus. Wenn wir die nicht-durchgestrichenen Kanten zurück zum Start verfolgen, haben wir also den schnellsten Weg gefunden.

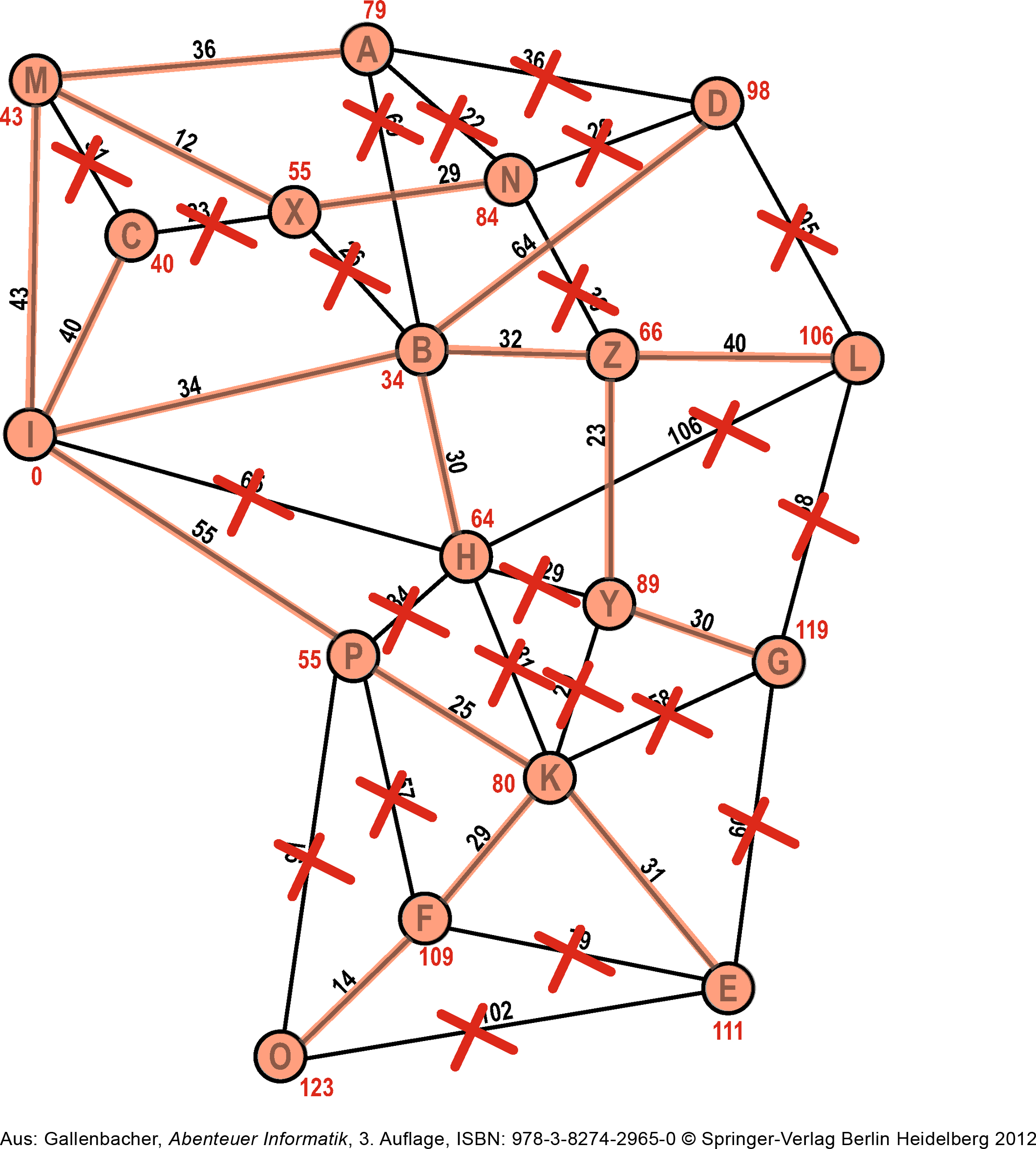
# Dijkstra

nach Jens Gallenbacher: Abenteuer Informatik

Wir wollen versuchen den «Ameisen»-Algorithmus für den Computer umzusetzen. Es macht nämlich wenig Sinn, sich gleichmässig auf den Kanten fortzubewegen. Wir kennen ja die Distanzen zwischen den Knoten. Statt zu schauen, welche Ameisen zuerst beim nächsten Knoten sind, wählen wir den «besten» Knoten von unserer Open-List und gehen dort weiter!

# Vorbereitung

Der Startknoten kommt auf die Open-List. Die zurückgelegte Distanz (von Startknoten zu Startknoten) ist natürlich 0.

Closed-List: –
  Open-List: I (0)

# Schritt 1

Wir fügen alle Nachbarn des Startknotens auf die Open-List. Dabei berechnen wir wie weit es vom Startknoten zum jeweiligen Knoten ist.
Ⓘ kommt auf die Closed-List.

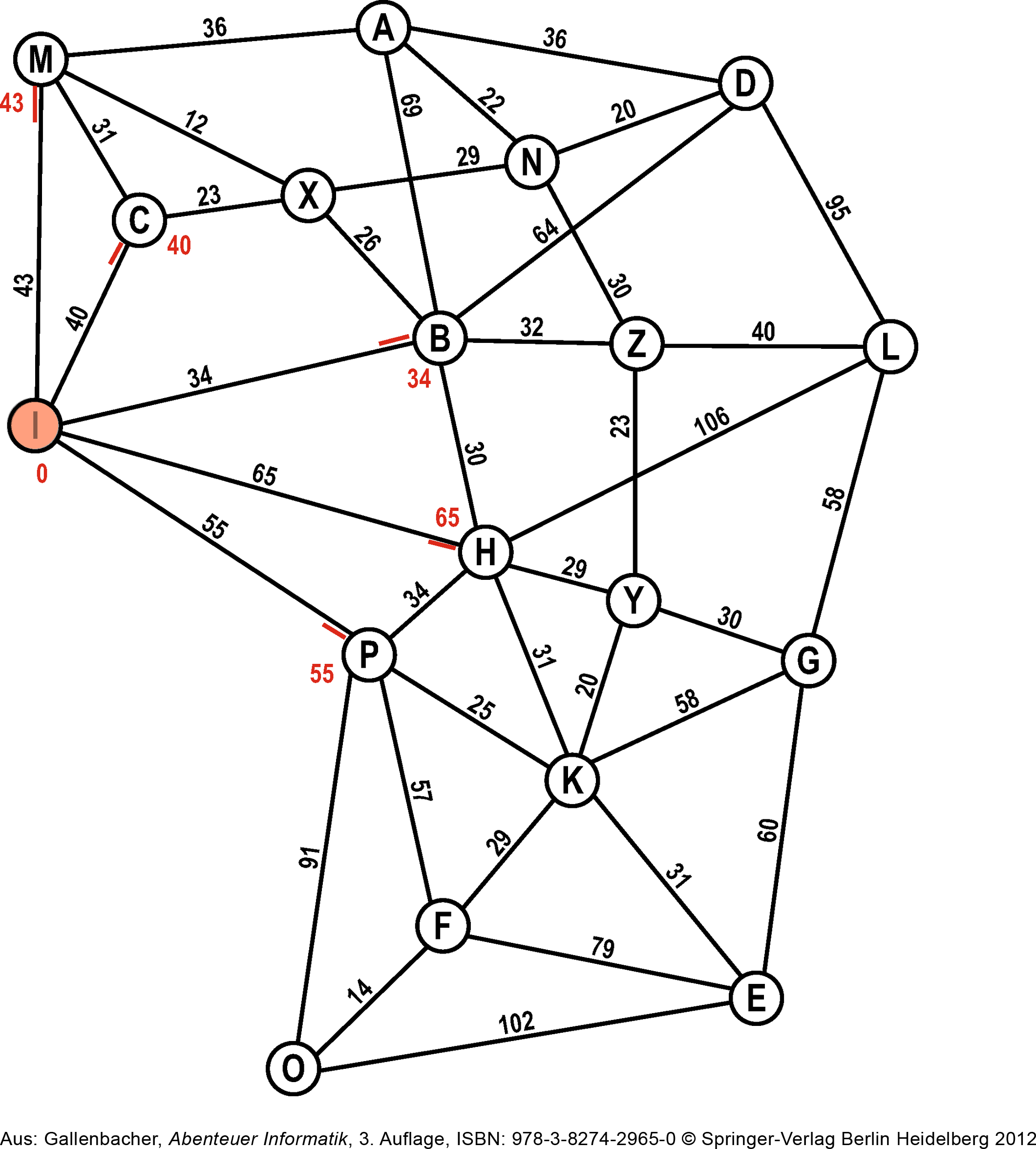
Closed-List: I
  Open-List: M (43), C (40), B (34), H (65), P (55)

# Vorbereitung Schritt 2

Wir suchen den besten Kandidaten aus unserer Open-List heraus. Der Knoten Ⓑ hat die kleinste Distanz, also machen wir dort weiter!

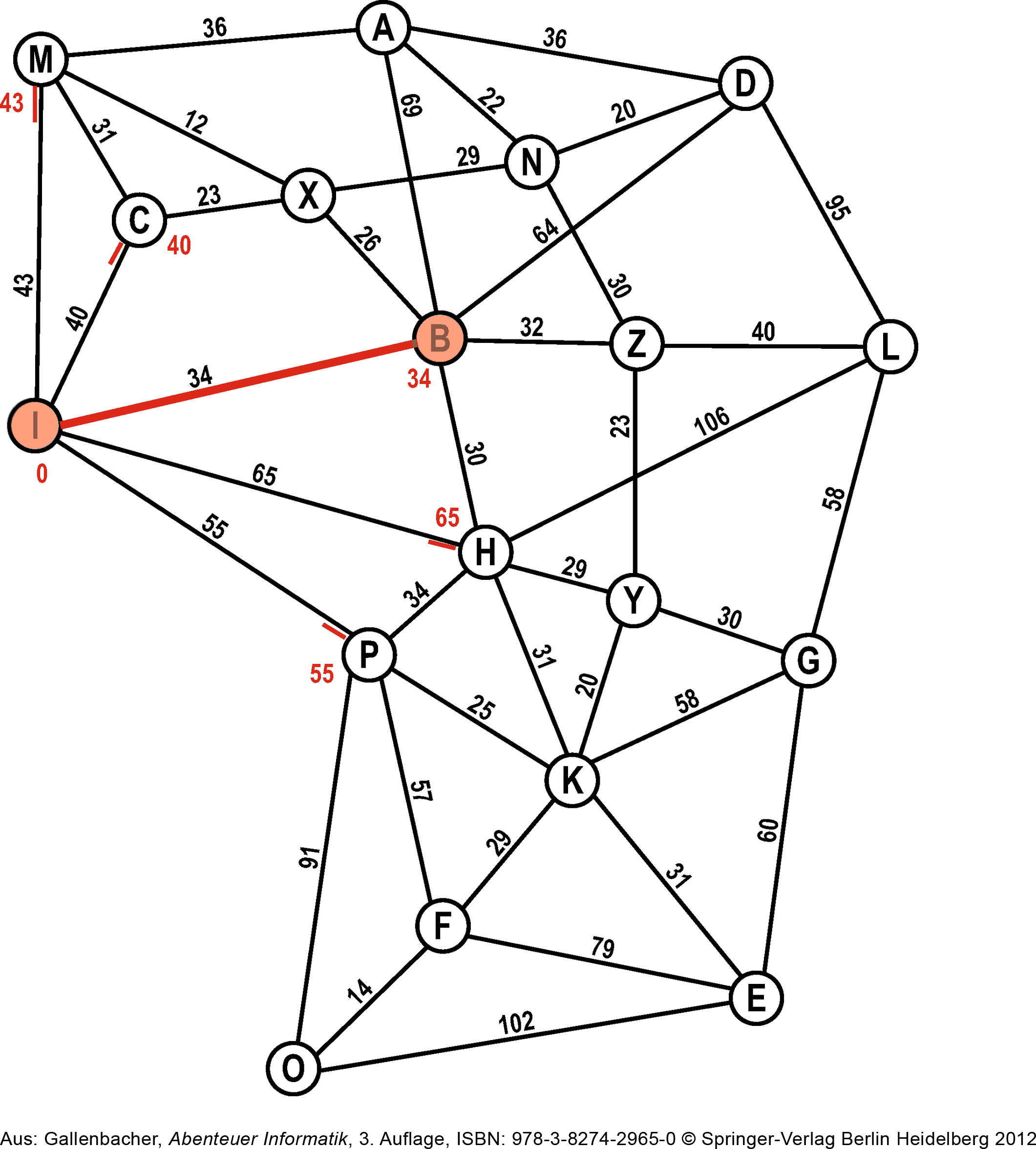
# Schritt 2

Wir berechnen für alle Nachbarn des Knotens Ⓑ ihre Distanz über vom Startknoten über Ⓑ. Ist der Knoten noch nicht auf der Open-List, wird dieser hinzugefügt. Ist ein Knoten – wie hier der Knoten Ⓗ – bereits auf der Open-List, schauen wir, ob wir einen kürzeren Weg gefunden haben. Wenn ja, aktualisieren wir den Knoten auf der Open-List.
Ⓑ kommt auf die Closed-List.

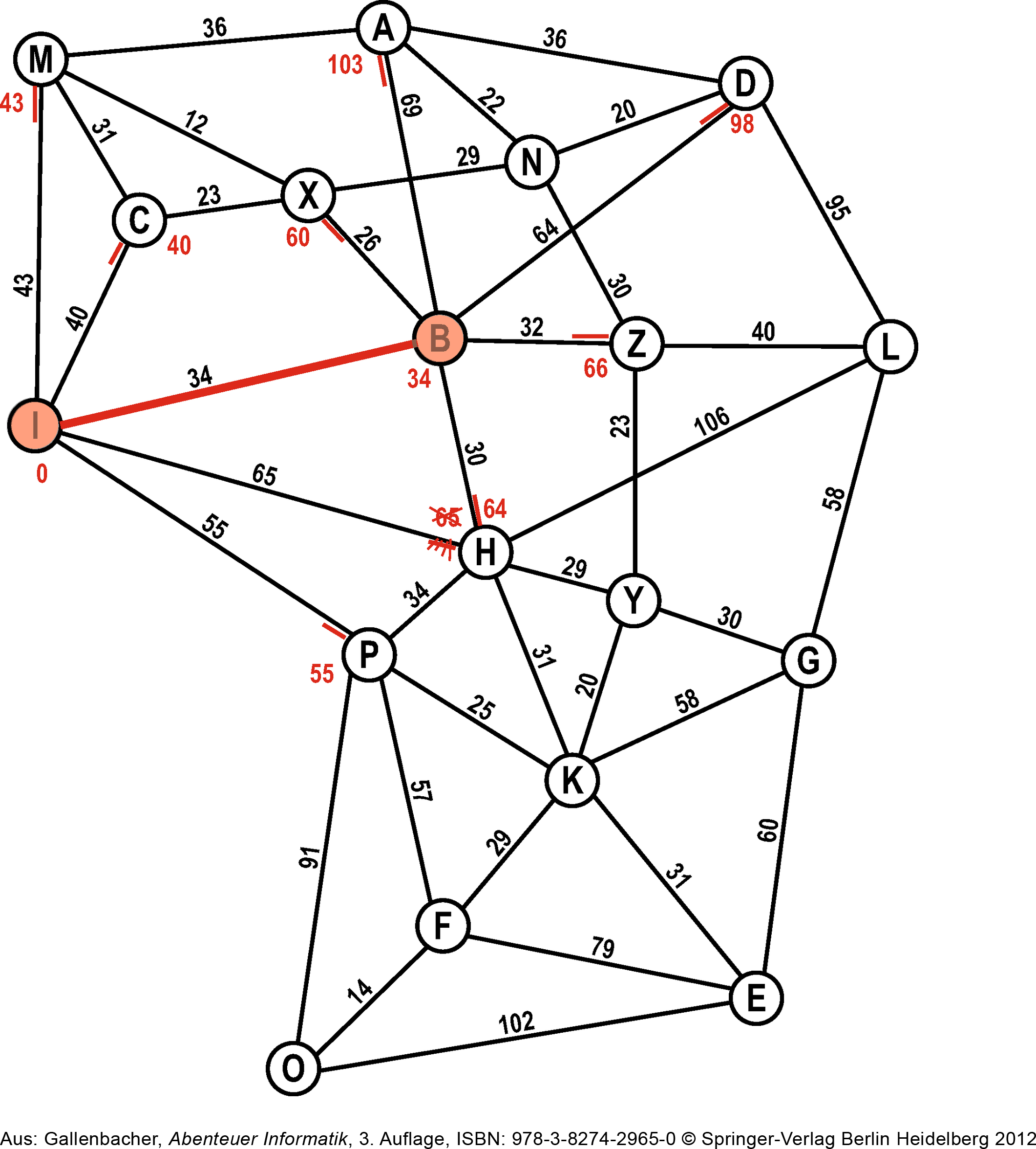
Closed-List: I, B
  Open-List: M (43), C (40), H (64), P (55), X (60), A (103), D (98), Z (66)

# Schritt 3

Der nächste «beste» Kandidat auf unserer Open-List ist Ⓒ. Die Nachbarn von Ⓒ sind aber bereits auf der Open-List – und zwar mit kürzerer Distanz als über Ⓒ.
Ⓒ kommt auf die Closed-List.

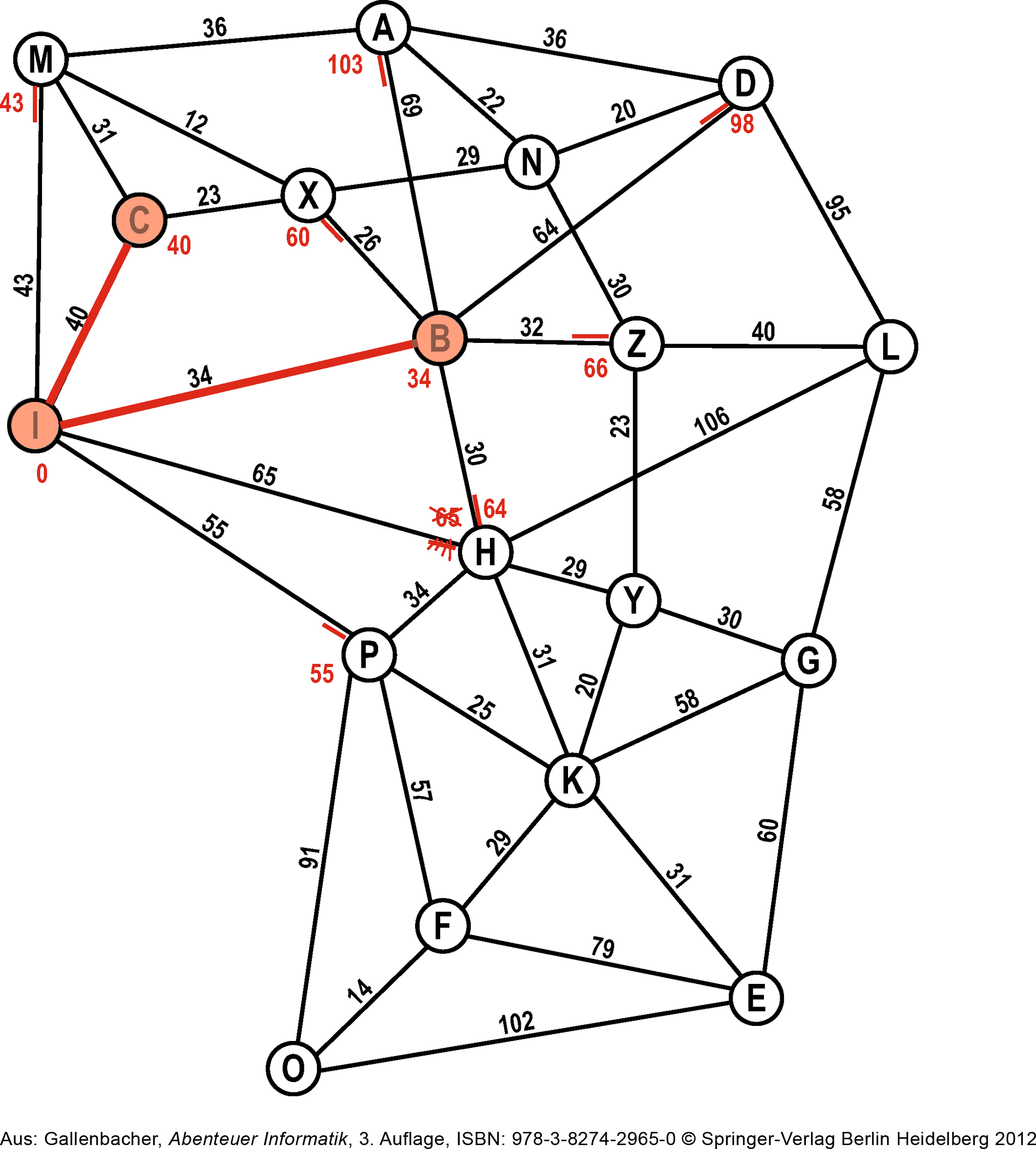
Closed-List: I, B, C
  Open-List: M (43), H (64), P (55), X (60), A (103), D (98), Z (66)

# Der Algorithmus

# Endzustand

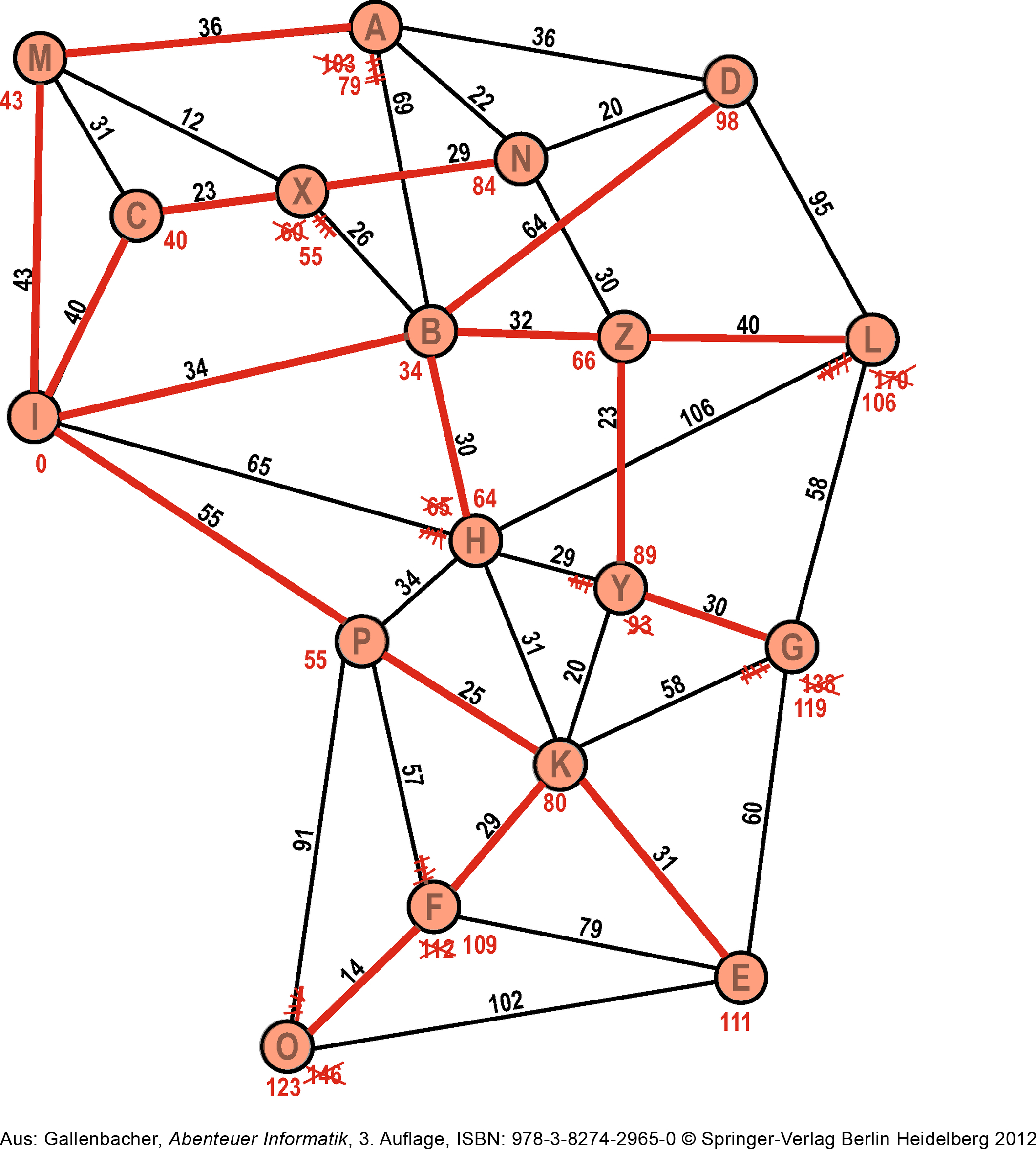
Wenn wir nur den besten Weg finden wollen, können wir den Algorithmus abbrechen, sobald der Zielknoten der «beste» Kandidat auf der Open-List ist. Dann wissen wir: Es gibt keinen kürzeren Weg! (Achtung: Wenn der Zielknoten nur auf der Open-List ist, könnte es immer noch einen besseren Weg geben!)
Wir können den Algorithmus auch weiterlaufen lassen. Am Schluss erhalten wir dann einen «Baum» (alle roten Kanten). Dieser Baum stellt die schnellsten Wege von Ⓘ zu jedem anderen Knoten des Graphen dar.

Aufgabe

Führe den Dijkstra-Algorithmus aus: Finde den kürzesten Weg in umgekehrter Richtung, also vom Knoten Ⓛ zum Knoten Ⓘ.

Zeichne dein Fortschritt analog zum Beispiel im Graphen auf
Führe daneben eine Open- und eine Closed-List

# Schilda

Das Ganze funktioniert auch für sogenannt «gerichtete Graphen»:

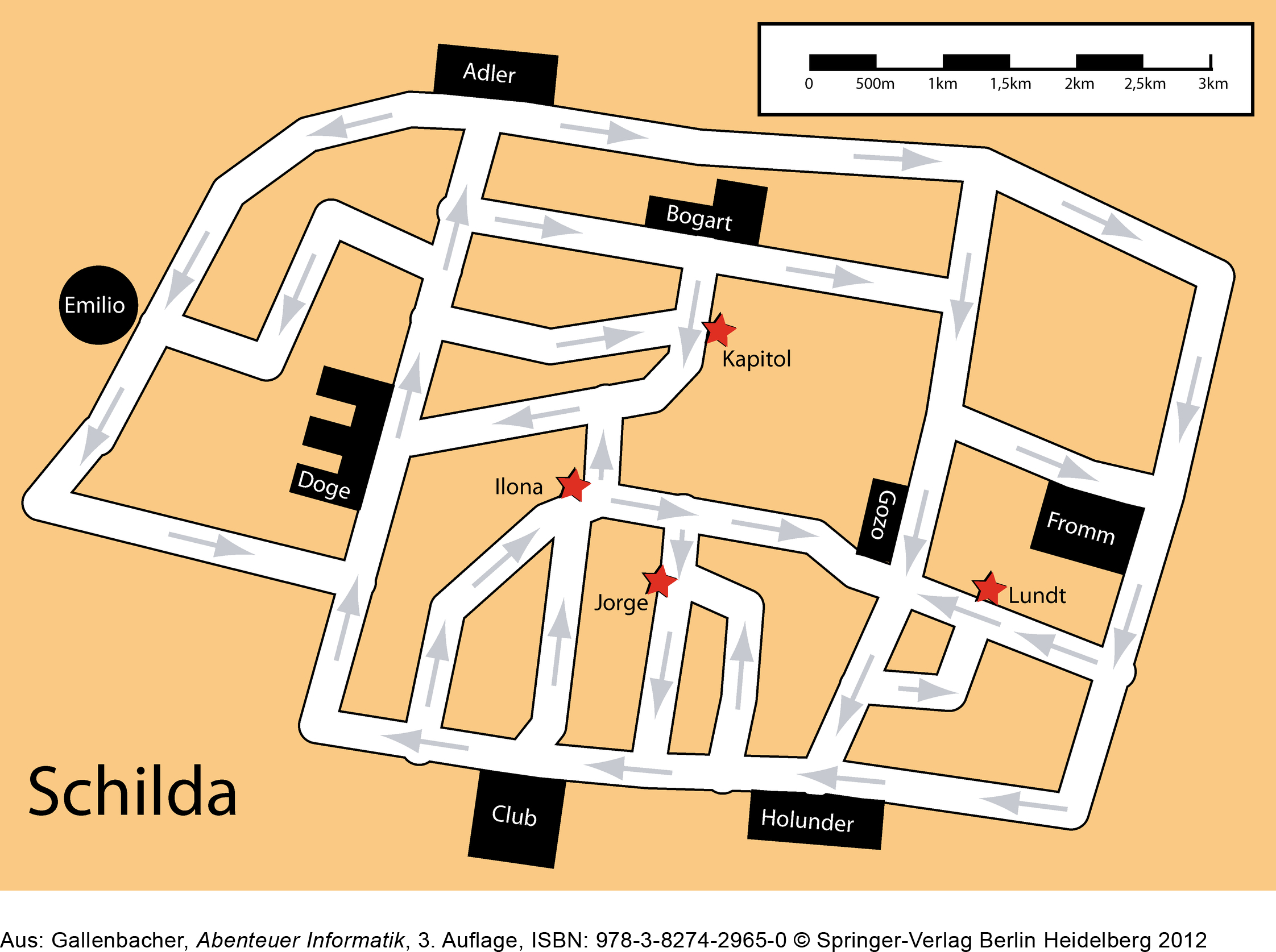
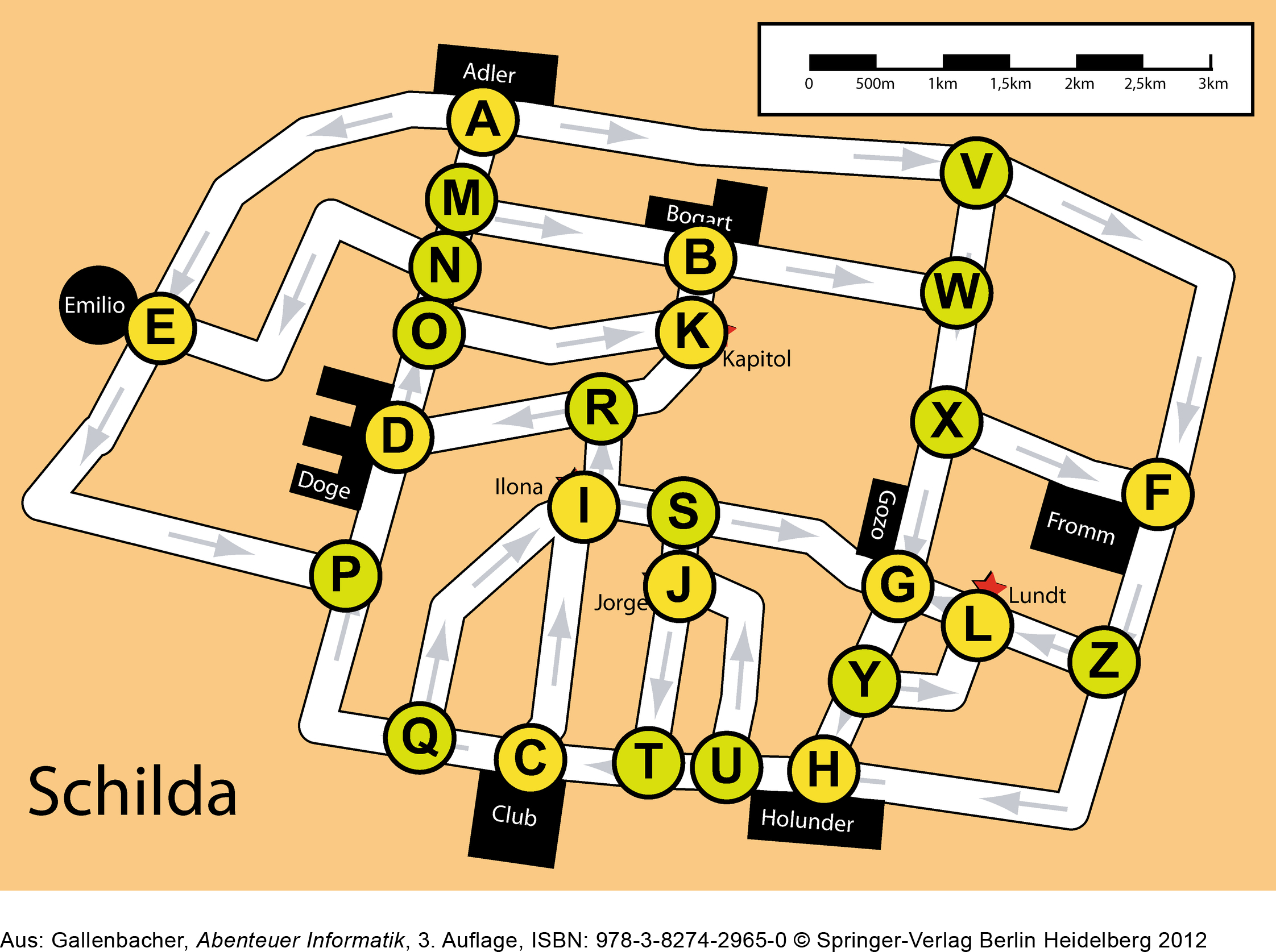
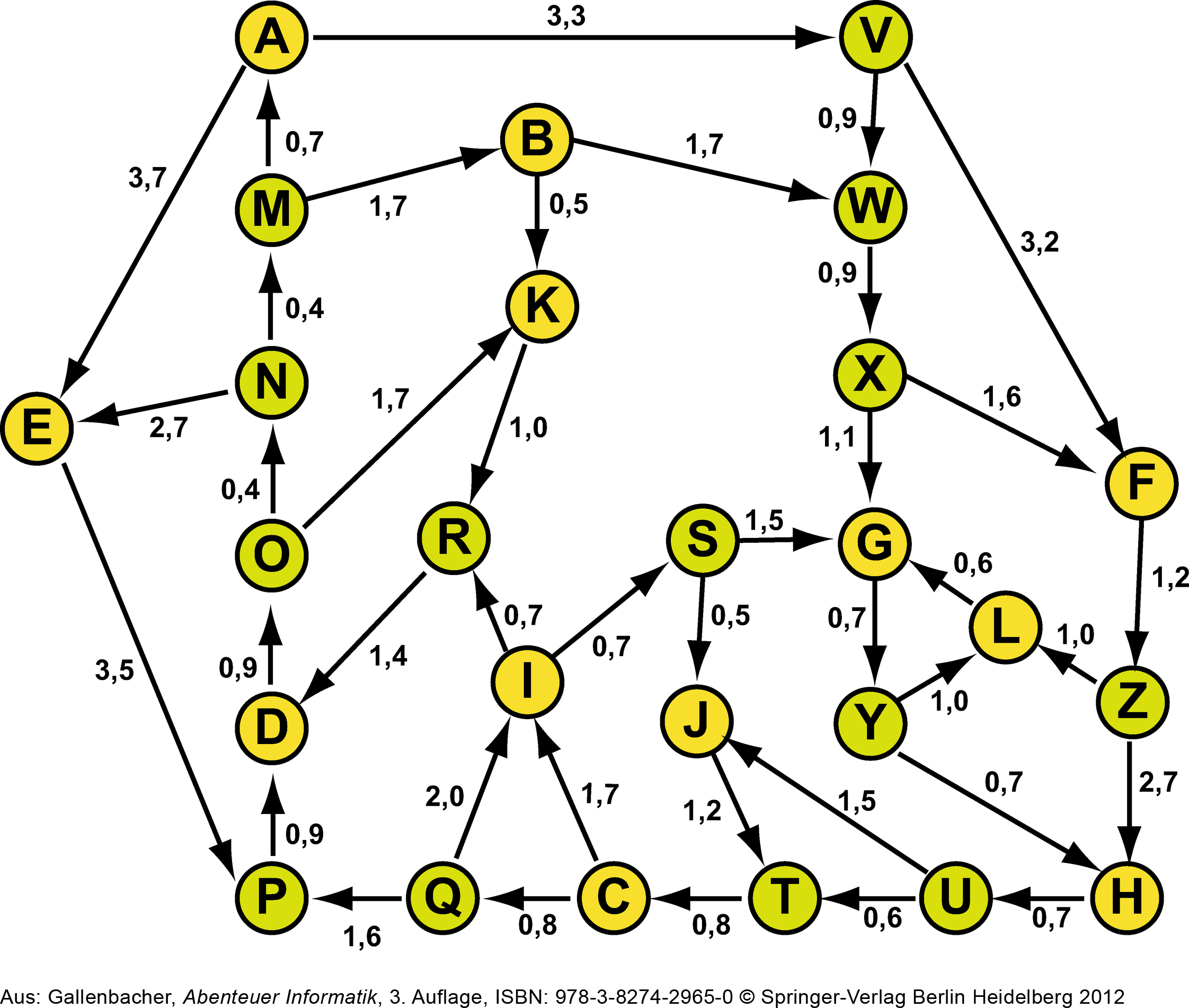
Aufgabe

Führe den Dijkstra-Algorithmus aus: erstelle eine Entfernungstabelle für das Hotel Adler. Finde die kürzesten Wege vom Knoten Ⓐ zu allen anderen Knoten.

Zeichne dein Fortschritt analog zum Beispiel im Graphen auf
Führe daneben eine Open- und eine Closed-List

# A-Stern

Der -Algorithmus^[2] (im folgenden genannt) wird verwendet um in einem Baum oder allgemein in einem Graphen den kürzesten Pfad zwischen zwei Knoten zu finden. Im Rahmen dieses Unterrichtsblocks wird der Einfachheit halber von einem Baum ausgegangen, allgemeinere Graphen werden nicht betrachtet. Um den anwenden zu können, müssen die Kanten des Baumes mit Kosten versehen sein. Gesucht ist nun der kürzeste (bzw. billigste) Pfad zwischen der Wurzel des Baumes und einem bestimmten Zielknoten.

Bei der Breiten- bzw. Tiefensuche wird keine «intelligente» Auswahl der Knoten in der Liste OPEN getroffen, die Knoten werden in willkürlicher Reihenfolge verarbeitet. Der ist eine Verfeinerung dieser Verfahren, wobei folgendermassen immer der vielversprechendste Knoten weiterverarbeitet wird. Es wird abgeschätzt, wie «gut» ein Knoten ist, indem eine Bewertungsfunktion berechnet wird. Die Kosten eines Knotens beinhalten zwei Beiträge: einerseits die Kosten vom Startknoten bis zu und andererseits die geschätzten Kosten von bis zum Zielknoten. Diese Bewertungsfunktion für einen Knoten wird also folgendermassen definiert:

Definition

, wobei
die Kosten des Pfades vom Startknoten zu darstellt und
die Kosten des optimalen Pfades von zu einem Zielknoten darstellt.

Dabei ist normalerweise unbekannt und kann nur abgeschätzt werden. Für dieses muss gelten: , wobei die wirklichen Kosten des optimalen Pfades von zu einem Zielknoten sind. Das heisst darf die Kosten eines Knotens nie überschätzen. Oft wird z.B. die euklidische Distanz zum Ziel verwendet.

Die Funktion ist eine sog. Heuristik, also eine Abschätzung des wahren Werts. So kann die Suche nach dem optimalen Pfad oft wesentlich beschleunigt werden, was beim ausgenutzt wird. Man kann zeigen, dass der immer den kürzesten Weg findet, wenn es einen gibt.

Beispiel

Wir suchen den schnellsten Weg von Würzburg nach Saarbrücken. Durch Abstraktion der Karte haben wir den folgenden gewichteten Graphen erhalten. Zusätzlich kennen wir für jeden Knoten eine Heuristik, nämlich die Distanz der Luftlinie nach Würzburg:

Karte	Aktion

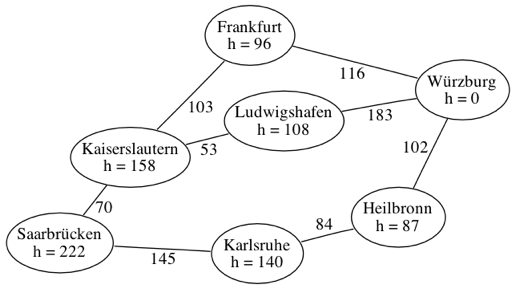Schritt 1

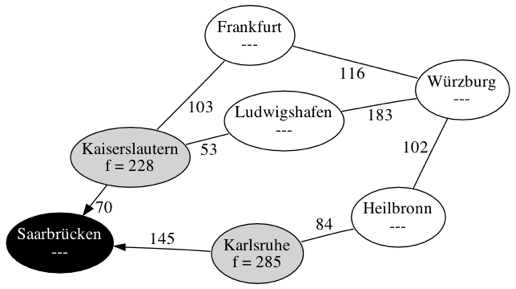Schritt 2

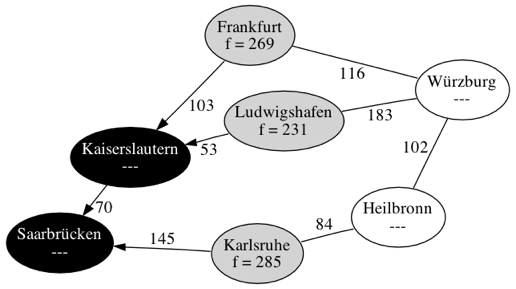Schritt 3

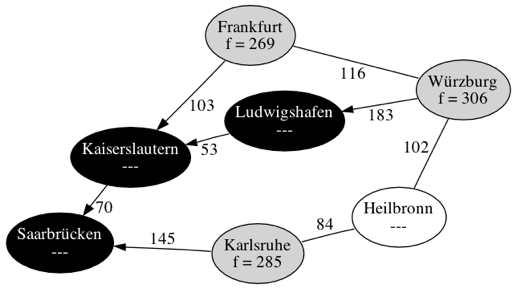Schritt 4

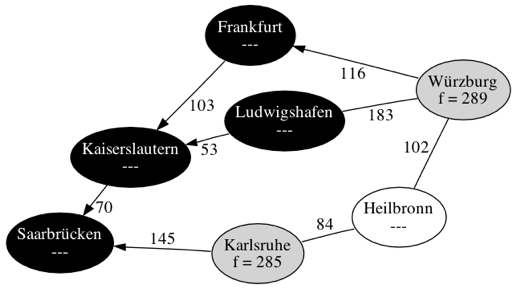Schritt 5

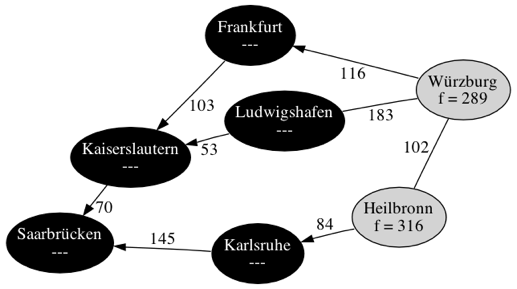Schritt 6

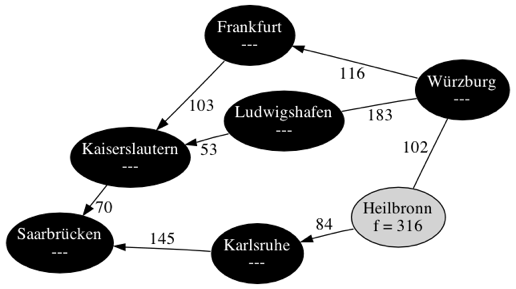Aufgabe

Beim Spiel «8-Puzzle» geht es darum, von einer beliebig durcheinander gebrachten Position der Zahlen durch Verschieben einzelner Zahlen in das jeweils leere Feld die folgende Zielposition zu erreichen:

Der -Algorithmus kann verwendet werden, um diese Aufgabe für beliebige Ausgangsstellungen zu lösen. Im Folgenden geht es darum, diesen algorithmischen Lösungsweg nachzuvollziehen und mit Suchverfahren ohne Heuristik zu vergleichen.

Finde mittels einer Tiefensuche (maximale Tiefe: 6) den Lösungsweg zur beschriebenen Zielposition aus der dargestellten Ausgangsstellung.
Vervollständige dazu den Suchbaum auf dem Zusatzblatt von links nach rechts bis der Zielknoten erreicht ist. Schreibe neben jeden Knoten die Reihenfolge, in welcher diese besucht werden (z.B. mit roter Farbe)
Denke dir eine Heuristik aus (d.h. definiere die Funktion ), um dieses Problem mit dem zu lösen. Diese Heuristik soll ein Mass dafür sein, wie nahe am Ziel der jeweilige Knoten ist.
Zeichne in den Suchbaum aus Aufgabe 1 ein, wie der mit deiner Funktion von Aufgabe 2 den Baum absuchen würde. Beginne beim Startknoten und berechne für alle Nachfolgeknoten
. Dabei ist die Anzahl bereits zurückgelegten Kanten. Verfolge immer denjenigen Nachfolgeknoten weiter, der den kleinsten Wert von hat. Schreibe neben jeden betrachteten Knoten den Wert der Funktion (z.B. so: (1) mit grün) und die Reihenfolge in welcher die Knoten besucht werden (z.B. <4> mit blau).
Ist der schneller als die Tiefensuche ohne Heuristik? Wie viele Knoten müssen besucht werden? Vergleiche diese Zahl mit denjenigen der Breiten- bzw. Tiefensuche.

-Algorithmus in Pseudocode

program a-star
   OPEN.add(startNode)
   repeat
      bestNode := OPEN.remove(Node with minimal f-Value)
      if (bestNode == targetNode) then return bestNode
      calcF(bestNode.successors())
      OPEN.add(bestNode.successors())
      CLOSED.add(bestNode)
   until (OPEN.isEmpty)
   return no path found
end

1
2
3
4
5
6
7
8
9
10
11

# Vergleich

	Breitensuche	Dijkstra	A-Stern

Ansatz	«Brute Force»	«Algorithmisch»	«Heuristisch»
Voraussetzung	normaler Graph	gewichteter Graph	gewichteter Graph inkl. Heuristik

https://commons.wikimedia.org/wiki/File:BinärBaum_Beschriftung.jpg (opens new window) ↩︎
Teile übernommen von Ryter, M.: Einführung in die künstliche Intelligenz. http://www.swisseduc.ch/informatik/theoretische_informatik/kuenstliche_intelligenz/ (opens new window) (26.12.2009) ↩︎

← Turing-Test Künstliche Neuronale Netze →