Im Folgenden wollen wir exemplarisch anschauen, wie Machine Learning mit Python funktionieren kann. Dazu verwenden wir ein Datenset, das sozusagen als «Hello-World»-Datenset des Machine Learnings gilt, das sogenannte Iris Flowers Dataset.
Dort wurden von 3 verschiedenen Schwertlilien-Arten je 50 Exemplare ausgemessen. Die Messerwert sind Länge und Breite des Kelchblatt (sepal) und Länge und Breite des Blütenblatts (petal).
Die Idee ist, dass die Daten in ein Trainings- und ein Validierungsset aufteilen und schauen, wie gut wir trainieren können und wie viele Blumen wir dann korrekt ihrer Art zuweisen können.
| Iris setosa | Iris versicolor | Iris virginica |
|---|---|---|
 |  |  |
Die Idee und die Quelltexte sind dem im August 2020 überarbeiteten englischsprachigen Artikel
«Your First Machine Learning Project in Python Step-By-Step» (opens new window) von Jason Brownlee entnommen.
# Herunterladen und installieren
# SciPy-Libraries
Voraussetzung für die folgenden Beispiele sind ein installierter Python-Interpreter und die folgenden fünf SciPy-Libraries:
- scipy
- numpy
- matplotlib
- pandas
- sklearn
Diese lassen sich wie gewohnt in Thonny unter Tools -> manage packages… hinzufügen oder updaten.
# Versionen überprüfen
Wir wollen kurz überprüfen, ob alles korrekt installiert ist. Kopiere das folgende Programm nach 1-check.py und starte es. Vergleiche deinen Output mit dem unten abgebildeten.
# Python version
import sys
print('Python: {}'.format(sys.version))
# scipy
import scipy
print('scipy: {}'.format(scipy.__version__))
# numpy
import numpy
print('numpy: {}'.format(numpy.__version__))
# matplotlib
import matplotlib
print('matplotlib: {}'.format(matplotlib.__version__))
# pandas
import pandas
print('pandas: {}'.format(pandas.__version__))
# scikit-learn
import sklearn
print('sklearn: {}'.format(sklearn.__version__))
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Die Versionen der Libraries sollten etwas gleich, oder geringfügig neuer sein. Der Output des Skripts sollte etwa wie folgt aussehen:
Python: 3.7.9 (v3.7.9:13c94747c7, Aug 15 2020, 01:31:08)
[Clang 6.0 (clang-600.0.57)]
scipy: 1.6.2
numpy: 1.20.2
matplotlib: 3.4.1
pandas: 1.2.4
sklearn: 0.24.1
Falls es einen Error gibt, so hast du etwas falsch gemacht – entweder etwas nicht richtig installiert, oder ev. eine falsche Version oder nicht ganz die korrekte Library.
# Daten laden
Wir laden nun das Blumenset direkt aus dem Internet. Es handelt sich um eine CSV-Datei, man kann diese auch im GitHub-Repo (opens new window) betrachten
# Die Libraries laden
Zuerst wollen wir aber sicherstellen, dass alle Pyhton-Libraries korrekt verfügbar sind. Dazu importieren wir alles was wir verwenden:
# Load libraries
from pandas import read_csv
from pandas.plotting import scatter_matrix
from matplotlib import pyplot
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
...
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Startet man dieses Programm sollte nichts geschehen. Wird aber ein Fehler angezeigt, so haben wir etwas nicht korrekt installiert und sollten das korrigieren.
# Das Datenset laden
Wir laden das Set übers Internet von der angegeben URL. Dazu verwenden wir die Library pandas, die wir dann auch noch zur Beschreibung der Daten verwenden könenn. Beim Import geben wir den Spalten der CSV-Datei gleich aussagekräftige Namen.
...
# Load dataset
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/iris.csv"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']
dataset = read_csv(url, names=names)
2
3
4
5
Jetzt sollten die Daten aus dem Internet geladen werden.
# Daten zusammenfassen
Jetzt können wir die Daten genauer anschauen.
In diesem Schritt werden wir die Daten aus verschiedenen Perspektiven betrachen:
- Dimension des Daten-Sets
- In die Daten reinschauen
- Statistische Zusammenfassung der Eigenschaften
- Klassen-Verteilung
Jede Perspektive ist ein Befehl. Diese Befehle sind aber hilfreich und können auch anderswo eingesetzt werden.
# Dimension des Daten-Sets
So erhalten wir einen Eindruck der Anzahl Einträge (Zeilen) und der Anzahl Eigenschaften (Spalten) des Datensets
...
# shape
print(dataset.shape)
2
3
Das Datenset hat 150 Einträge mit je 5 Eigenschaften:
(150, 5)
# In die Daten reinschauen
Es kann nicht schaden einige Datensätze anzuschauen. Der folgende Befehl stellt die ersten 20 Einträge dar:
...
# head
print(dataset.head(20))
2
3
Die 20 Zeilen sollten wie folgt aussehen:
sepal-length sepal-width petal-length petal-width class
0 5.1 3.5 1.4 0.2 Iris-setosa
1 4.9 3.0 1.4 0.2 Iris-setosa
2 4.7 3.2 1.3 0.2 Iris-setosa
3 4.6 3.1 1.5 0.2 Iris-setosa
4 5.0 3.6 1.4 0.2 Iris-setosa
5 5.4 3.9 1.7 0.4 Iris-setosa
6 4.6 3.4 1.4 0.3 Iris-setosa
7 5.0 3.4 1.5 0.2 Iris-setosa
8 4.4 2.9 1.4 0.2 Iris-setosa
9 4.9 3.1 1.5 0.1 Iris-setosa
10 5.4 3.7 1.5 0.2 Iris-setosa
11 4.8 3.4 1.6 0.2 Iris-setosa
12 4.8 3.0 1.4 0.1 Iris-setosa
13 4.3 3.0 1.1 0.1 Iris-setosa
14 5.8 4.0 1.2 0.2 Iris-setosa
15 5.7 4.4 1.5 0.4 Iris-setosa
16 5.4 3.9 1.3 0.4 Iris-setosa
17 5.1 3.5 1.4 0.3 Iris-setosa
18 5.7 3.8 1.7 0.3 Iris-setosa
19 5.1 3.8 1.5 0.3 Iris-setosa
# Statistische Zusammenfassung der Eigenschaften
Mit einem einfachen Befehl erhalten wir von jeder Eigenschaft eine Zusammenfassung über das ganze Datenset bestehend aus Anzahl, Mittelwert, Standardabweichung, Minimum und Maximum sowie 3 Perzentilen:
...
# descriptions
print(dataset.describe())
2
3
An Hand der Ausgabe sehen wir, dass alle Werte dieselbe Einheit haben und sich im selben Bereich (zwischen 0 und 8 Zentimetern) bewegen.
sepal-length sepal-width petal-length petal-width
count 150.000000 150.000000 150.000000 150.000000
mean 5.843333 3.054000 3.758667 1.198667
std 0.828066 0.433594 1.764420 0.763161
min 4.300000 2.000000 1.000000 0.100000
25% 5.100000 2.800000 1.600000 0.300000
50% 5.800000 3.000000 4.350000 1.300000
75% 6.400000 3.300000 5.100000 1.800000
max 7.900000 4.400000 6.900000 2.500000
# Klassen-Verteilung
Wir zählen die Anzahl Einträge für jede Blumen-Art, also alle Zeilen welche unter class denselben Eintrag haben:
...
# class distribution
print(dataset.groupby('class').size())
2
3
Wir sehen, dass jede Klasse (also jede Blumenart) gleich viele Einträge im Datenset hat (nämlich 50 oder ein Drittel).
class
Iris-setosa 50
Iris-versicolor 50
Iris-virginica 50
# Komplettes Beispiel
Wenn wir alles bis jetzt zusammenfassen erhalten wir das folgende Skript:
from pandas import read_csv
# Load dataset
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/iris.csv"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']
dataset = read_csv(url, names=names)
# shape
print(dataset.shape)
# head
print(dataset.head(20))
# descriptions
print(dataset.describe())
# class distribution
print(dataset.groupby('class').size())
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Daten visualisieren
Wir haben nun einen ersten Einblick in unsere Daten erhalten. Diesen wollen wir nun mit Hilfe von grafischen Darstellungen vertiefen.
Wir werden zwei Arten von Diagrammen erstellen:
- Eindimensionale Plots, damit wir die einzelnen Eigenschaften besser verstehen
- Mehrdimensionale Plots, damit wir die Abhängigkeiten zwischen den Eigenschaften erkennen können
# Eindimensionale Plots
Wir beginnen mit eindimensionalen Diagrammen. Dies ergibt jeweils für jede Eigenschaft eine Grafik.
# Box-Plots
Unsere Daten sind alle numerisch. Wir können also die Verteilung der Werte einer Eigenschaft mit dem sogenannten *Box-Plot *veranschaulichen:
...
# box and whisker plots
dataset.plot(kind='box', subplots=True, layout=(2,2), sharex=False, sharey=False)
pyplot.show()
2
3
4
Das Ergebnis sieht wie folgt aus:
Box-Plot
Beim Box-Plot werden die Werte eindimensional dargestellt. Dabei befinden sich 50% aller Werte im Kästchen, die anderen gehen bis zu den Antennen. Einzelne Ausreisser sind mit kleinen Kreischen gekennzeichnet. Die Linie im Kästchen steht für den Median. (mehr (opens new window))
# Histogramm
Wir können auch für jede Eigenschaft ein Histogramm erstellen:
...
# histograms
dataset.hist()
pyplot.show()
2
3
4
Wir erkennen, dass zwei Eigenschaften mehr oder weniger eine Gauss-Verteilung (schöne Kurve) liefern. Andere Eigenschaften sehen eher wie «Kamelbuckel» aus, was auf Unterschiede zwischen den Blumenarten hinweist.
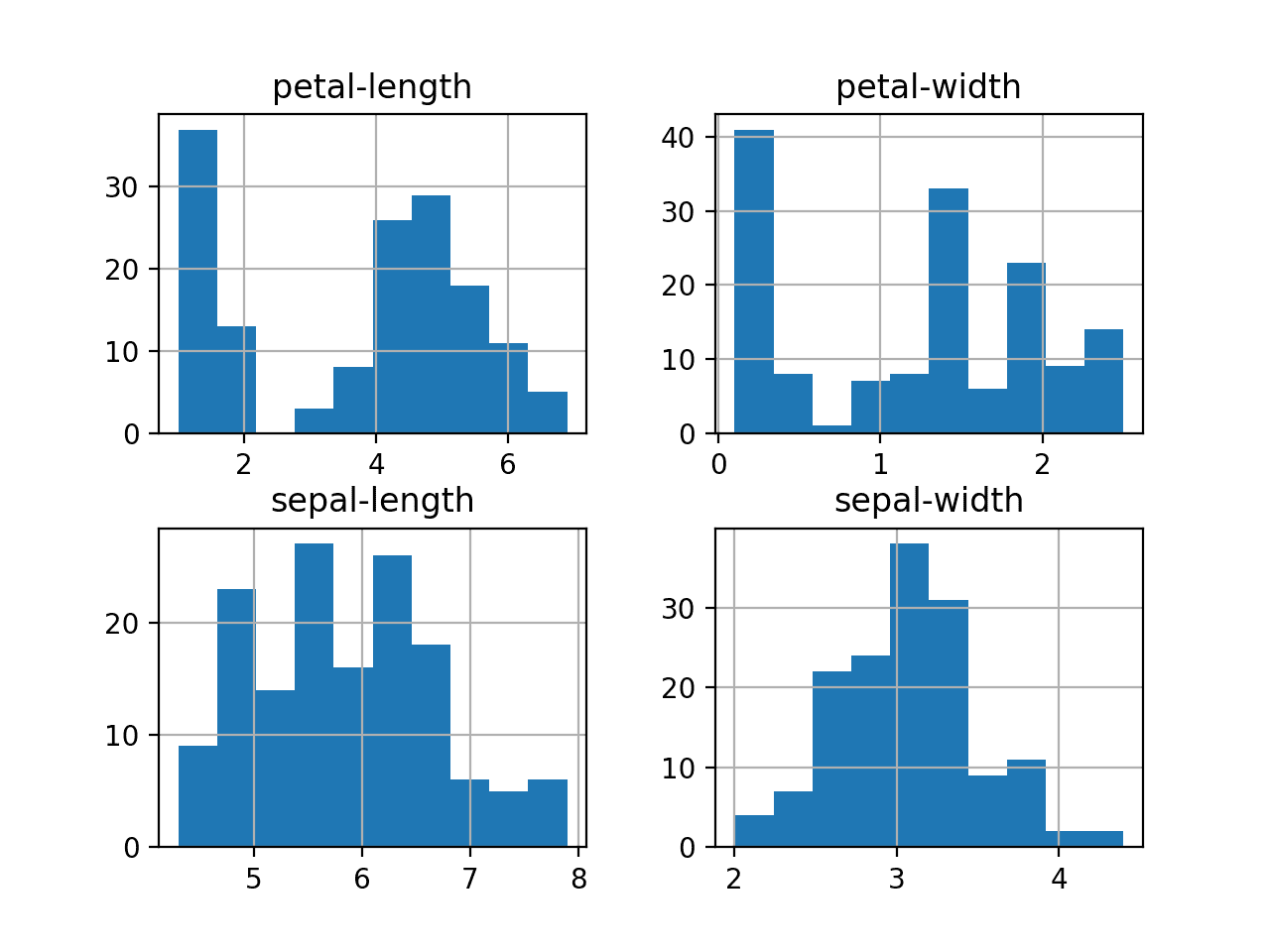
Histogramm
Das Histogramm stellt die Häufigkeitsverteilung grafisch dar. Dazu müssen die Werte in Klassen eingeteilt werden, also z.B. alle Blätter mit einer Breite zwischen 5.0 und 5.5 cm. Diese werden gezählt und ihre Anzahl in der y-Achse dargestellt. (mehr (opens new window))
# Mehrdimensionale Plots
Nun wollen wir noch die Abhänigkeiten zwischen den Eigenschaften betrachten.
Dazu erstellen wir Scatterplots für alle möglichen Kombinationen zweier Eigenschaften:
...
# scatter plot matrix
scatter_matrix(dataset)
pyplot.show()
2
3
4
Die diagonale Gruppierung bei einigen Scatterplots weist auf einen starken Zusammenhang der Eigenschaften hin und somit auch auf eine gute Voraussagbarkeit.
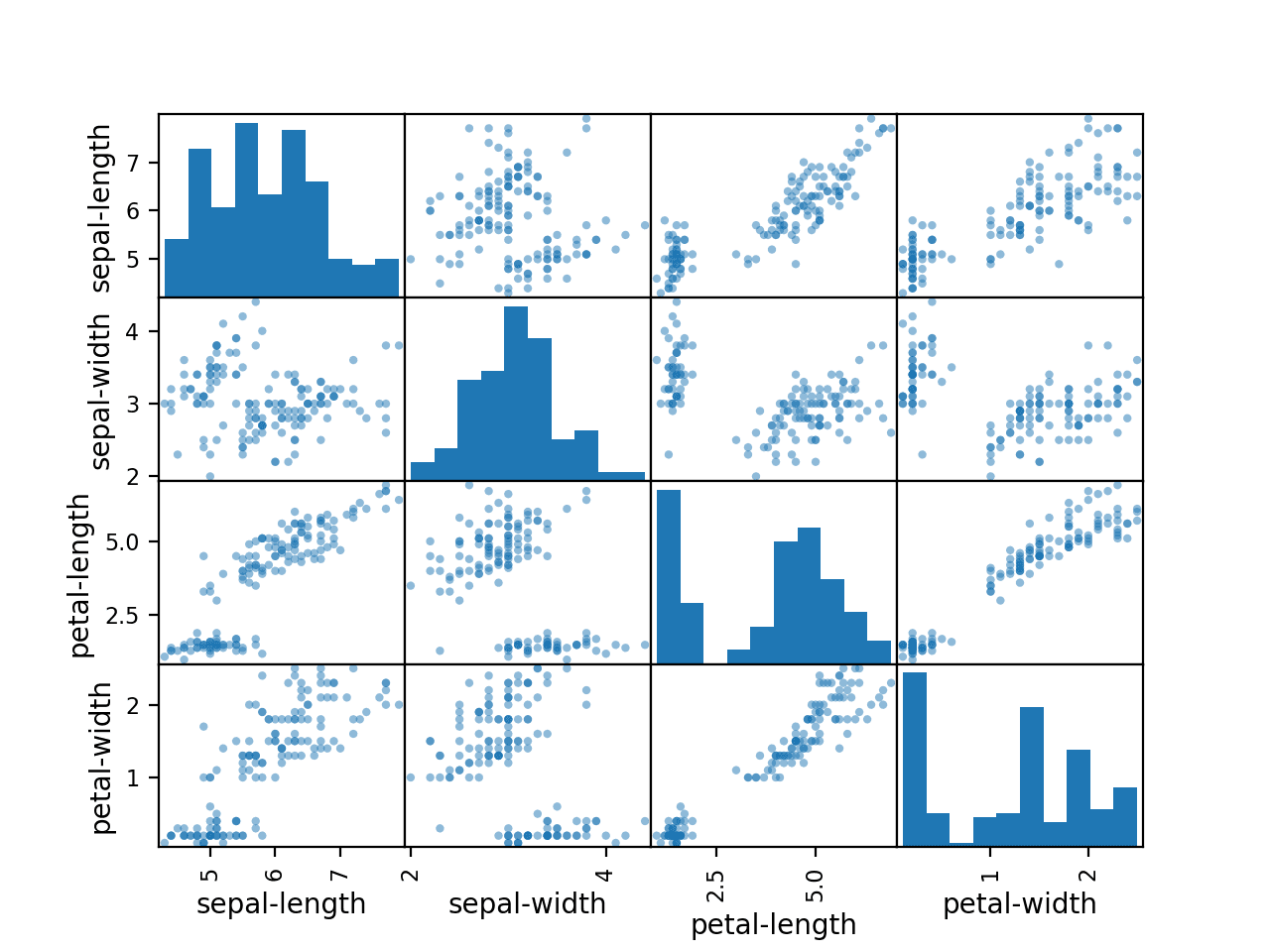
Scatter Plot (Streudiagramm)
Beim Scatter Plot werden die Wertepaare als Punkte in einem kartesischen Koordinatensystem dargestellt. Es ergibt sich eine Punktwolke. Je näher sich zwei Punkte befinden, umso ähnlicher sind ihre Werte. (mehr)
# Komplettes Beispiel
Wenn wir das Visualisierungs-Kapitel zusammenfassen erhalten wir das folgende Skript:
# visualize the data
from pandas import read_csv
from pandas.plotting import scatter_matrix
from matplotlib import pyplot
# Load dataset
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/iris.csv"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']
dataset = read_csv(url, names=names)
# box and whisker plots
dataset.plot(kind='box', subplots=True, layout=(2,2), sharex=False, sharey=False)
pyplot.show()
# histograms
dataset.hist()
pyplot.show()
# scatter plot matrix
scatter_matrix(dataset)
pyplot.show()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Algorithmen evaluieren
Nun ist es an der Zeit mit den Daten einige Modell zu erstellen und ihre Genauigkeit auf unbekannte Daten abzuschätzen.
Dazu gehen wir wie folgt vor:
- Ein Validierungs-Set extrahieren
- Die Testumgebung für 10-fold cross validation vorbereiten
- Mehrere verschiedene Modell erzeugen um die Blumen-Art aus den Messwerten vorauszusagen
- Das beste Modell auswählen
# Das Validierungs-Set erzeugen
Wir müssen abschätzen können, wie gut unser erzeugtes Model ist. Dazu müssen wir einen Teil der Daten aussondern, damit wir diese später zur Validierung verwenden können.
Wir unterteilen das Set in zwei Teile: 80% der Daten werden zum Trainieren verwendet. 20% werden als Validation-Set zurückbehalten.
...
# Split-out validation dataset
array = dataset.values
X = array[:,0:4]
y = array[:,4]
X_train, X_validation, Y_train, Y_validation = train_test_split(X, y, test_size=0.20, random_state=1)
2
3
4
5
6
Nun haben wir die Trainingsdaten in X_train und Y_train. Die Validierungsdaten die wir später verwenden sind in X_validation und Y_validation.
# Testumgebung
Wir verwenden eine «geschichtete» 10-fold cross validation um die Genauigkeit des Modells zu bestimmen.
Dadurch wird unser Datenset in 10 Teile unterteilt. Mit 9 Teilen wird trainiert und mit dem 10. Teil wird getestet. Das wird für alle Kombinationen wiederholt –
jeder Teil darf also mal der letzte Teil sein.
«Geschichtet» heisst hier, dass jeder der 10 Teile die gleiche Verteilung der Blumen-Arten hat wie das gesamte Datenset aufweist.
Zum Bewerten der Modelle verwenden wir die accuracy. Dabei handelt es sich um den Prozentsatz der korrekt vorausgesagten Blumen.
# Modelle erzeugen
Wir wissen nicht, welche Algorithmen die besten Ergebnisse für unser Problem liefern. Wir testen mal die folgenden 6 Algorithmen:
- Logistic Regression (LR)
- Linear Discriminant Analysis (LDA)
- K-Nearest Neighbors (KNN).
- Classification and Regression Trees (CART).
- Gaussian Naive Bayes (NB).
- Support Vector Machines (SVM).
Das ist ein guter Mix aus einfachen linearen (LR und LDA) und nicht-linearen (KNN; CART, NB und SVM) Algorithmen.
Wir erzeugen also diese 6 Modelle und evaluieren diese.
...
# Spot Check Algorithms
models = []
models.append(('LR', LogisticRegression(solver='liblinear', multi_class='ovr')))
models.append(('LDA', LinearDiscriminantAnalysis()))
models.append(('KNN', KNeighborsClassifier()))
models.append(('CART', DecisionTreeClassifier()))
models.append(('NB', GaussianNB()))
models.append(('SVM', SVC(gamma='auto')))
# evaluate each model in turn
results = []
names = []
for name, model in models:
kfold = StratifiedKFold(n_splits=10, random_state=1, shuffle=True)
cv_results = cross_val_score(model, X_train, Y_train, cv=kfold, scoring='accuracy')
results.append(cv_results)
names.append(name)
print('%s: %f (%f)' % (name, cv_results.mean(), cv_results.std()))
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Das beste Modell auswählen
Wir haben nun 6 Modelle erzeugt und eine Schätzung der Genauigkeit für jedes Modell. Wir vergleichen nun die Modelle miteinander und bestimmen das genauste.
Wenn wir den obenstehenden Code ausführen erhalten wir:
LR: 0.960897 (0.052113)
LDA: 0.973974 (0.040110)
KNN: 0.957191 (0.043263)
CART: 0.957191 (0.043263)
NB: 0.948858 (0.056322)
SVM: 0.983974 (0.032083)
Hinweis
Deine eigenen Ergebnisse können von den hier dargestellten abweichen. Der Grund dafür ist die Zufallskomponente beim StratifiedKFold.
Es sieht so aus, als ob Support Vector Machines (SVM) mit 98% die höchste Genauigkeit liefert.
Wir können die Resultate aber auch grafisch darstellen und so die Verteilung und die Druchschnittsgenauigkeit der Modelle visualisieren. Dies ist möglich, weil jeder Algorithmus 10x ausgeführt worden ist (mit der 10 fold-cross validation).
Ein sinnvoller Weg die Resultate zu vergleichen ist ein Box-Plot für jede Verteilung.
...
# Compare Algorithms
pyplot.boxplot(results, labels=names)
pyplot.title('Algorithm Comparison')
pyplot.show()
2
3
4
5
Wir sehen dass sich die Boxen weit oben befinden, mit vielen Genauigkeiten bei 100% und nur einigen die runter bis ca. 82% gehen.
# Komplettes Beispiel
Das komplette Beispiel zur Evaluation der Algorithmen:
# compare algorithms
from pandas import read_csv
from matplotlib import pyplot
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import StratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
# Load dataset
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/iris.csv"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']
dataset = read_csv(url, names=names)
# Split-out validation dataset
array = dataset.values
X = array[:,0:4]
y = array[:,4]
X_train, X_validation, Y_train, Y_validation = train_test_split(X, y, test_size=0.20, random_state=1, shuffle=True)
# Spot Check Algorithms
models = []
models.append(('LR', LogisticRegression(solver='liblinear', multi_class='ovr')))
models.append(('LDA', LinearDiscriminantAnalysis()))
models.append(('KNN', KNeighborsClassifier()))
models.append(('CART', DecisionTreeClassifier()))
models.append(('NB', GaussianNB()))
models.append(('SVM', SVC(gamma='auto')))
# evaluate each model in turn
results = []
names = []
for name, model in models:
kfold = StratifiedKFold(n_splits=10, random_state=1, shuffle=True)
cv_results = cross_val_score(model, X_train, Y_train, cv=kfold, scoring='accuracy')
results.append(cv_results)
names.append(name)
print('%s: %f (%f)' % (name, cv_results.mean(), cv_results.std()))
# Compare Algorithms
pyplot.boxplot(results, labels=names)
pyplot.title('Algorithm Comparison')
pyplot.show()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# Voraussagen machen
Um Voraussagen zu machen, müssen wir einen Algorithmus wählen.
Die Resultate des vorherigen Abschnitts sprehcen für SVM als das genauste Modell. Wir werden dieses als unser endgültiges Modell verwenden.
Nun wollen wir die Genauigkeit des Modells auf unser Validation-Set anschauen.
Dadurch erhalten wir einen unabhängigen Blick auf die Genauigkeit des besten Modells. Es ist wertvoll ein Validation-Set aufzusparen, falls beim Training ein Overfitting auftritt.
# Voraussagen machen
Wir verwenden nun das gesammete Trainings-Set und machen dann die Voraussage mit dem Validierungs-Set.
...
# Make predictions on validation dataset
model = SVC(gamma='auto')
model.fit(X_train, Y_train)
predictions = model.predict(X_validation)
2
3
4
5
# Voraussagen evaluieren
Wir können die Voraussagen evaluieren, indem wir sie mit den erwarteten Ergebnis vergleichen. Daraus berechnen wir die Klassifikations-Genauigkeit, die Verwechlsungs-Matrix und den Klassifikations-Report.
....
# Evaluate predictions
print(accuracy_score(Y_validation, predictions))
print(confusion_matrix(Y_validation, predictions))
print(classification_report(Y_validation, predictions))
2
3
4
5
Wir sehen dass die Genauigkeit 96% beträgt.
Die Verwechslungs-Matrix gibt Anhaltspunkte zu den gemachten Fehlern.
Schlussendlich liefert der Klassifikations-Report eine Zusammenfassung zu jeder Klasse.
Alles in allem ein sehr gutes Ergebnis!
0.9666666666666667
[[11 0 0]
[ 0 12 1]
[ 0 0 6]]
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 11
Iris-versicolor 1.00 0.92 0.96 13
Iris-virginica 0.86 1.00 0.92 6
accuracy 0.97 30
macro avg 0.95 0.97 0.96 30
weighted avg 0.97 0.97 0.97 30
# Komplettes Beispiel
Der komplette Code des letzten Kapitels:
# make predictions
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn.svm import SVC
# Load dataset
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/iris.csv"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']
dataset = read_csv(url, names=names)
# Split-out validation dataset
array = dataset.values
X = array[:,0:4]
y = array[:,4]
X_train, X_validation, Y_train, Y_validation = train_test_split(X, y, test_size=0.20, random_state=1)
# Make predictions on validation dataset
model = SVC(gamma='auto')
model.fit(X_train, Y_train)
predictions = model.predict(X_validation)
# Evaluate predictions
print(accuracy_score(Y_validation, predictions))
print(confusion_matrix(Y_validation, predictions))
print(classification_report(Y_validation, predictions))
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28