Aufgabe nach Ralf Kretzschmar «Künstliche Intelligenz für echte Fische»
In dieser Übung befassen Sie sich mit der automatisierten Datenauswertung auch «Data Mining» genannt. Dazu werden Sie nach einigen Vorüberlegungen ein Verfahren testen, welches zur Familie der «künstlichen Intelligenz» gehört. Obwohl Sie weder das Verfahren noch seine Funktionsweise kennen, können Sie durch einige Überlegungen und empirischen Tests heraustüfteln, wo die Möglichkeiten und Grenzen dieses Verfahrens liegen.
# Die Aufgabe
Die junge isländische Hochseefischerin Sigrún ist es leid, oftmals unter widrigen Bedingungen die gefangenen Fische von Hand zu sortieren (siehe Abb.1). Sigrún hat mitbekommen, dass Sie sich gerade mit Data-Mining befassen. Daher fragt sie Sie an, ob Sie ihr helfen würden, einen Fischsortierapparat zu entwickeln. Selbstverständlich wollen Sie Sigrún nicht im Stich lassen!



# Fische für Apparat und Magen
Im Allgemeinen wird ein Apparat bzw. Algorithmus der Gruppen von Dingen, Werten, etc. unterscheiden bzw. klassifizieren kann als «Classifier» bezeichnet.
Egal wie unser Fischsortierapparat auch immer aussehen mag, es macht sicherlich Sinn den Apparat mit echten Fischen zu testen oder besser noch echte Fische als Vorlage in den Entwicklungsprozess des Apparats mit einzubeziehen. Sigrún hat Ihnen aus diesem Grund zahlreiche, nach Sorten angeschriebene Hering und Lodder Fische zukommen lassen. Damit die Fische anschliessend nicht im Abfall landen, hat Sigrún ihre Lieblingsrezepte für Hering und Lodder beigelegt.
# Versuch mit einer Messgrösse
Ein Apparat der zwei Fischsorten unterscheiden soll, braucht mindestens eine Messgrösse zur Orientierung. Übersteigt für einen Fisch diese Messgrösse einen gewissen Grenzwert, in der Fachsprache Threshold genannt, so wird entschieden, dass der Fisch zur einen Fischsorte gehört, wenn nicht, zur anderen. Je besser sich die beiden Fischsorten durch diese Messgrösse unterscheiden lassen, desto besser funktioniert der Apparat.
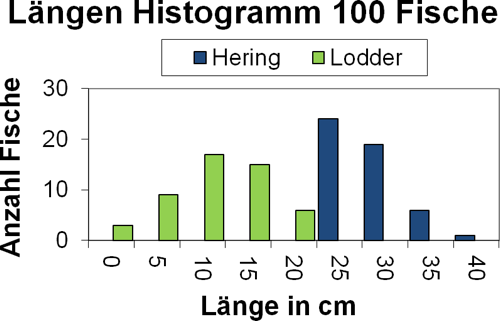
Als Beispiel schauen wir uns als fiktive Messgrösse die Länge der Fische an. Abb.4 zeigt das Längen Histogramm von 50 Hering und 50 Lodder Fischen, welche Sie Sigrúns Lieferung entnommen haben. Aus den Histogrammen können Sie herauslesen, wie viele Fische von jeder Sorte im jeweiligen Längenintervall zu liegen kommen.
- Frage 1
- Wählen Sie für das Histogramm in Abb.4 einen möglichst guten Threshold. Schätzen Sie den ungefähren prozentualen Fehler ab, den der Apparat bei der Unterscheidung von Hering und Lodder voraussichtlich machen wird.
- Frage 2
- Etwas am Histogramm in Abb.4 müsste Ihnen komisch vorkommen. Warum ist das Resultat aus Frage 1 vermutlich zu gut um wahr zu sein? Und wie könnte man das Problem in Abb.4 beheben? Formulieren Sie erst Ihre Ideen bevor Sie weiterlesen.
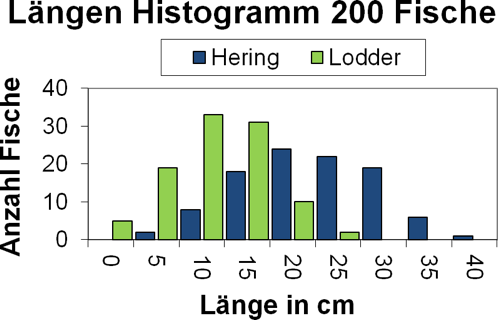
Sigrún meint es gut mit Ihnen und schickt prompt eine zweite Lieferung von 50 Hering und 50 Lodder Fischen. Auch diese neuen Fische vermessen Sie und fügen Sie den 100 Fischen im Histogramm in Abb.4 hinzu. Daraus resultiert das Histogramm in Abb.5
- Frage 3
- Wählen Sie auch für das Histogramm in Abb.5 einen möglichst guten Threshold. Schätzen Sie den ungefähren prozentualen Fehler ab, den der Apparat bei der Unterscheidung von Hering und Lodder voraussichtlich machen wird.
- Frage 4
- Wenn man einen Classifier zur Unterscheidung irgendwelcher Dinge (hier Fische) möchte, auf was muss man bezüglich der Auswahl dieser Dinge achten? Vergleichen Sie dazu die beiden Histogramme in Abb.4 und Abb.5 und formulieren Sie einen Rat.
# Versuch mit zwei Messgrössen
Allein aufgrund der Länge lässt sich Hering nicht exakt von Lodder trennen. Basierend auf Abb.5 dürfte man nur Fische
Ihre Aufgabe: Überlegen Sie sich eine zusätzliche Messgrösse zur realistischen Unterscheidung von Hering und Lodder. Berücksichtigen Sie dabei, dass sich die Grösse möglichst einfach auf einem Schiff messen lassen sollte. Kreative Lösungen sind durchaus erwünscht.
In der Praxis ist die Wahl solcher Messgrössen von entscheidender Bedeutung. Ein Classifier «sieht» nicht die zu unterscheidenden Dinge selber, sondern nur ihre Messgrössen. Da diese Messgrössen die einzige Informationen darstellen, welche in den Classfier eingehen, bezeichnet man diese Messgrössen als «Input Features». Sind die Input Features charakteristisch für das Klassifikationsproblem, so darf man auf eine gute Klassifizierung hoffen, sind die Input Features unspezifisch für das Klassifikationsproblem, so ist von einer schlechten Klassifizierung auszugehen (z.B. wären die aktuellen Schweizer Lottozahlen zum Zeitpunkt des Fangs schlechte Input Features für den Fischsortierapparat).
Für Abb.6 a) wurden zwei verschiedene, fiktive Messgrössen (
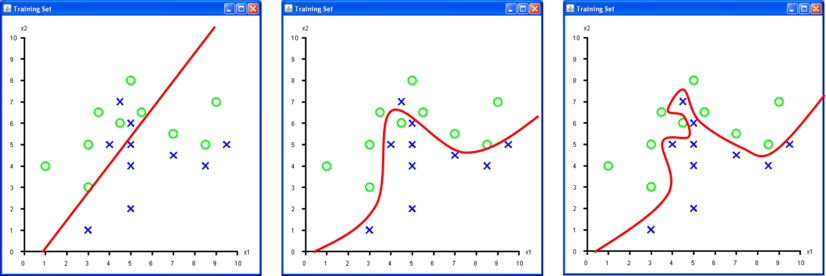
Den «Raum» welchen die Input Features «aufspannen» nennt man «Input Feature Space». Das Histogramm in Abb.4 stellt einen ein-dimensionalen Input Feature Space dar, Abb.6 a) einen zwei-dimensionalen. Höher-dimensionale Input Feature Spaces (z.B. 100-dimensional oder mehr) sind nicht unüblich, jedoch nicht mehr vernünftig als Bild darstellbar.
- Frage 5
- Welche Decision Boundary in Abb.6 ist die Beste und warum? Beantworten Sie die Frage bevor Sie weiterlesen!
Wie Sie gesehen haben, wird ein Set von Daten (hier Fische) verwendet, um einen Classifier für seine Aufgabe «einzustellen». Dieses Set von Daten wird als «Training Set» bezeichnet. Um entscheiden zu können, ob die Decision Boundary des Classifiers nach dessen «Einstellung» vernünftig gewählt ist, braucht es ein zweites, vom ersten unabhängiges Set von Daten, das «Validation Set». In Abb.7 stellt die obere Zeile a), b) und c) das Training Set aus Abb.6 dar. Die untere Zeile Abb.7 d), e) und f) zeigt dieselben Decision Boundaries für ein unabhängiges Validation Set (d.h. für 2×10 weitere Fische).
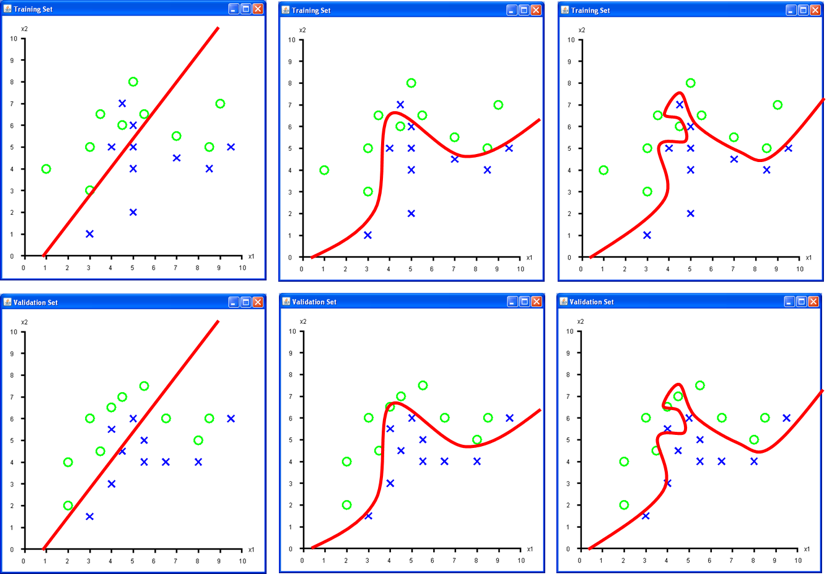
Tab.1 vergleicht für jede Decision Boundary die Training und Validation Sets. «Anzahl Falsche» zählt alle Fische, welche falsch klassifiziert werden, d.h. welche sich auf der falschen Seite der Decision Boundary befinden. Ist dieser «Klassifikationsfehler» für beide Sets in etwa gleich, wird von guter «Generalisierung» gesprochen. Dann kann davon ausgegangen werden, dass alle künftigen Daten (hier künftige Fische) ähnlich gut oder schlecht klassifiziert werden.
«Overfitting» drückt aus, wie stark eine Decision Boundary von einzelnen Datenpunkten beeinflusst wird, d.h. wie stark ein Classifier die einzelnen Datenpunkte im Training Set «auswendig gelernt hat». Starkes Overfitting bedeutet starkes Auswendiglernen.
Die «Komplexität» der Decision Boundary lässt sich grob mit der möglichen Anzahl von «Krümmungen» beschreiben. Ist die Komplexität zu tief, lässt sich der Zusammenhang zwischen Input Features und Klassenzuordnung nicht darstellen, ist die Komplexität zu hoch, besteht die Gefahr von Overfitting.
| Abb.7 a) & d) | Abb.7 b) & e) | Abb.7 c) & f) | |
|---|---|---|---|
| Anzahl Falsche Training | 6 | 2 | 0 |
| Anzahl Falsche Validation | 5 | 2 | 4 |
| Generalisierung | gut | gut | schlecht |
| Overfitting | leicht | leicht | stark |
| Komplexität | zu tief | gut | zu hoch |
# Übersicht Verfahren
Wie wird die Decision Boundary bestimmt? Im Wesentlichen ist die Decision Boundary der Graph einer mathematischen Funktion, welche mehrere freie Parameter enthält. Die Art der Funktion und die Wahl deren freier Parameter bestimmt die Lage und Form der Decision Boudary. Grob lassen sich folgende drei Methodenfamilien unterscheiden.
# Statistische Methoden
Hierbei wird die «Verteilung» aller Datenpunkte einer jeden Klasse mit einer separaten Funktion geschätzt (z.B. mit einem Histogramm oder einer Dichtefunktion, z.B. Normalverteilung). Die freien Parameter werden basierend auf den vorhandenen Datenpunkten berechnet. Aus diesen Verteilungen lässt sich direkt die «optimale» Decision Boundary mittels statistischer Formeln bestimmen.
# Stochastische Methoden
Dafür wird eine Funktion mit hinreichend vielen freien Parametern genommen, alle Parameter per Zufallsgenerator immer und immer wieder bestimmt, bis eine hinreichend gute Decision Boundary gefunden oder die Geduld zuende ist. Moderne Verfahren dieser Art suchen im ganzen Input Feature Space nach guten Treffern und konzentrieren sich dann auf die Umgebung dieser Treffer.
# Iterative Methoden
Wie bei den stochastischen Methoden werden alle freien Parameter einer Funktion in einem Initialisierungsschritt per Zufallsgenerator bestimmt. Danach werden die freien Parameter so verändert (d.h. die Decision Boundary verschoben und verformt), dass der Fehler über dem Training Set leicht abnimmt. Dieser Adaptionsschritt wird mehrfach wiederholt, bis keine signifikante Verbesserung mehr eintritt. Der ganze Prozess inklusive Initialisierung wird mehrfach wiederholt, um nach Lösungen von mehreren Stellen im Input Feature Space aus zu suchen.
# Bemerkungen
# 1. Fehlerfunktion
Keine Methode «löst das Problem» direkt, es wird eine Fehlerfunktion minimiert! Am Ende wird derjenige Classifier gewählt, welcher den kleinsten Fehlerwert aufweist. Passt die Fehlerfunktion gut zum eigentlichen Problem, darf gehofft werden; passt die Fehlerfunktion nicht zum eigentlichen Problem, so wird etwas ganz anderes «gelöst».
# 2. Overfitting
Alle Methoden neigen ab einer gewissen Anzahl freier Parameter zu Overfitting. Ebenso benötigen alle Methoden gute Input Features und repräsentative Daten.
Zugeschnittenes Foto. Original: fish0191 von David Csepp, NOAA/NMFS/AKFSC/Auke Bay Lab., auf https://www.flickr.com/ (opens new window), Abgerufen 20.7.14, Lizenz: CC-BY-2.0 ↩︎
Scan of Culpea Harengus, from Schlegel, H (Hermann), 1869, Natuurlijke Historie van Nederland – De Visschen, Amsterdam, G.L. Funke, collected by en:User:Citron auf http://commons.wikimedia.org (opens new window), Abgerufen 20.7.14, Lizenz: Public Domain ↩︎
Scan of Mallotus Villosus, from Evermann, B.W. and E.L. Goldsborough, 1907. The fishes of Alaska. Bull. U.S. Bur. Fish via FishBase, collected by en:User:Stan Shebs auf http://commons.wikimedia.org (opens new window), Abgerufen 20.7.14, Lizenz: Public Domain ↩︎
← KNN mit Excel Prüfung →